Тема. Лінії на площині.

План

1. Рівняння лінії на площині.

2. Рівняння прямої на площині.

3. Рівняння прямої з кутовим коефіцієнтом.

4. Рівняння прямої.

5. Рівняння прямої,яка проходить через дану точку в даному напрямі.

6. Канонічне рівняння прямої.

7. Рівняння прямої, що проходить через дві задані точки.

8. Рівняння прямої у відрізках

9. Загальне рівняння прямої.

10. Взаємне розміщення двох прямих.

Ключові поняття і терміни:

- площина,

- пряма,

- відрізок.

Література:

1. Грисенко М.В., Математика для економістів.-К.: «Либідь»,- 2007р.,

стор. 7-44.

2. Рудавський Ю.К., Костробій П.П., Д.В.Уханська, Лінійна алгебра та аналітична геометрія.-Л.: «Бескід Біт»,-2002р., стор.7-54.

3. Овчинников П.П., Яремчук Ф.П., Михайленко В.М., Вища математика, ч.1.,-К.: «Техніка»,-2003р., стор. 23-34.

4. Лейфура В.М., Голодницький Г.І., Файст Й.І., Математика.-К.: «Техніка», -2003р., стор. 264-298.

5. Пономаренко О.І., Перестюк М.О., Бурим В.М., Основи математичної економіки.-К.: «Інформ техніка», -1995р.

Рівняння лінії на площині

> Означення: Рівняння лінії (кривої) на площині називають рівняння з двома змінними х та у, яке задовольняють координати^ довільної точки цієї лінії й не задовольняють координати будь-якої точки, що не лежить на цій лінії

У загальному випадкові рівняння лінії L записується так:

• F(х,у) = 0.

Іноді змінну у можна виразити з рівняння (3.1); тоді

рівняння лінії має вигляд

y=f(x)

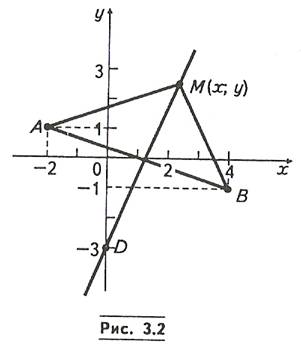
■ Приклад 1. Запишемо рівняння лінії точок, рівновіддалених від двох точок площини А (-2; 1) і В(4; -1).

Відстань між двома точками M1 (x1;y1) M2 (x2;y2) визначається за

формулою

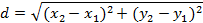(3.3)

Нехай А/(х; y) — довільна точка шуканої лінії

(рис.3.2). Тоді, підставляючи координати точок М(х у),

А(-2; І), В(4; -1) у формулу (3.3) і прирівнявши відстані,

матимемо

Піднесемо до квадрата обидві частини рівняння. Після перетворень дістанемо

Зх-7- 3 = 0,

Або

у= Зх-3

.Це рівняння прямої MD, що є серединним перпендикуляром до від­різка А В.

Взагалі можна записати рівняння будь-якої лінії, але на практиці це не завжди просто зробити.

Щоб переконатися, чи належить точка М(х₀; у₀) даній лінії L, рівняння якої F(x, у) = 0, треба перевірити, чи задовольняють коорди­нати цієї точки дане рівняння.

Дата добавления: 2015-07-20