Gоф(t)~sвх(t0-t) .

Примем t0=Тс,отклик ОФ повторяет по форме АКФ входного сигнала

Sвых(t)~Кs_вх(t-Tc).

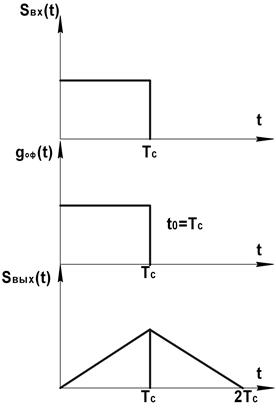
Известно, что импульсная характеристика – это реакция цепи на δ-импульс.

Подберем структуру фильтра, дающего отклик на δ-импульс требуемой формы

Здесь -идеальный интегратор;

-идеальная линия задержки;

-идеальный вычитатель.

Проверим, соответствует ли эта схема требованием ФСОВИ. Две проверки:

1. Подадим δ-импульс, получим импульсную характеристику.

2. Подаем сигнал, получаем АКФ.

Проверка подтверждает оптимальность фильтра.

Но реализация такого оптимального фильтра невозможна, так как невозможно построить идеальный интегратор, идеальную линию задержки и идеальный вычитатель.

Рассмотрим возможность синтеза ФСОВИ по требуемой частотной характеристике оптимального фильтра.

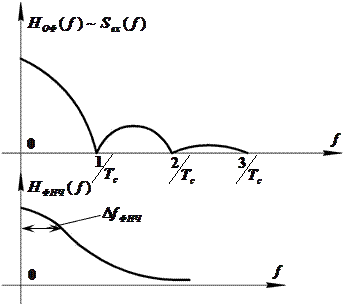
Реализация АЧХ оптимального фильтра для прямоугольного импульса является невозможной. Поэтому заменим оптимальный фильтр квазиоптимальным – ФНЧ, АЧХ которого приведена на рисунке, где Δf_фнч – полоса пропускания ФНЧ.

Замена оптимального фильтра фильтром НЧ приводит к уменьшению отношения сигнал -шум на выходе фильтра.

Проигрыш ФНЧ оптимальному фильтру в отношении сигнал-шум зависит от выбора полосы пропускания Δf_фнч.

Наименьший проигрыш ФНЧ оптимальному фильтру в отношении сигнал-шум получается при полосе пропускания 0.2/Т_с и равен 18.5%.

Попробуем объяснить, почему таким образом изменяется эта зависимость:

Рассмотрим три ситуации:

1) Δf_фнч<

2) Δf_фнч=

3) Δf_фнч>

Им соответствуют три отклика ФНЧ:

В первом случае сигнал на выходе не достигает пикового значения. В третьем случае сигнал на выходе достигает пикового значения, как и во втором, но из-за большой полосы пропускания фильтра мощность шума на выходе больше чем во втором случае. Наилучший вариант второй.

Заметим, что кроме проигрыша в отношении сигнал/шум, ФНЧ дает отклик длительностью примерно на 60 % больше, чем оптимальный фильтр.

Дата добавления: 2015-07-20