Доверительные интервалы (пределы) для генеральной средней

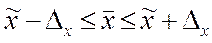
Доверительные интервалы (пределы) для генеральной доли

2. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки.

Для расчета объема выборки необходимо знать дисперсию либо долю в генеральной совокупности. Они заменяются величинами, полученными в предшествующих обследованиях или при пробных малых выборках. В случаях, если W даже приблизительно определить невозможно, в расчет вводят максимальную величину дисперсии доли, равную 0,25 (если W = 0,5, то W (1-W) = 0,25).

Приведем примеры расчетов генеральных характеристик и численности выборки при простом случайном бесповторном отборе.

На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за месяц:

Месячный доход, руб	до 1500	1500-2500	2500-3500	более 3500
Число рабочих

Следует определить: 1) среднемесячный размер дохода у работников этого предприятия, гарантируя результат с вероятностью 0,997; 2) долю рабочих предприятия, имеющих месячный доход 2500 руб. и выше, гарантируя результат с вероятностью 0,954; 3) необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 100 руб.; 4) необходимую численность выборки при определении доли рабочих с размером месячного дохода 2500 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 4%.

Решение:

1. Доверительный интервал (пределы) среднего размера месячного дохода работников предприятия:

Предельная ошибка выборки D_x= tm_x

При вероятности 0,997 t = 3 (см. таблицу Лапласа)

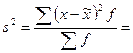((1000-2640)² * 12 + (2000-2640)² *20 +(3000-2640)² * 60 + (4000-2640)² *8) / 100 =147968

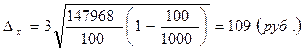
2640 – 109 £ £ 2640 + 109

2531 £ £ 2749

Таким образом, с вероятностью 0,997 (т.е. в 997 случаях из 1000) можно утверждать, что средний месячный доход у работников данного предприятия находится в пределах от 2531 до 2749 рублей.

2. W – доля рабочих, имеющих месячный доход 2500 руб. и выше

Предельная ошибка для доли D_p= tm_p=

При вероятности Р = 0,954 t = 2

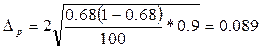
0,68 – 0,089 £ p £ 0,68 + 0,089

0,591 £ p £ 0,769

или

59,1% £ p £ 76,9%

В 95,4% случаях можно гарантировать, что доля рабочих, имеющих размер месячного дохода 2500 руб. и выше, находится от 59,1% до 76,9 % всех рабочих данного предприятия.

3. Необходимая численность выборки для определения среднего месячного дохода определяется по формуле:

По условию задачи известны:

при вероятности 0,954 t = 2

D_x= 100 руб.

s² = 147968 (по данным предыдущей выборки)

чел.

Необходимая численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка не превышала 100 руб., равна 56 человек.

4. Необходимая численность выборки для определения доли рабочих, имеющих доход 2500 руб. и выше, определяется по формуле:

По условию задачи известны:

при вероятности 0,954 t = 2

= 4% или 0,04

W = 0,68 (по данным предыдущей выборки)

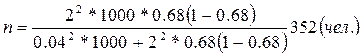
Необходимая численность выборки для определения доли рабочих с размером месячного дохода 2500 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 4%, равна 352 человека из тысячи рабочих данного предприятия.

Механическая выборка заключаетсяв отбореединиц из генеральной совокупности через равные промежутки из определенного расположения их в генеральной совокупности, (по алфавиту, в пространстве, последовательности появления во времени)

При организации механического отбора вначале определяют так называемый шаг отсчета, т.е. расстояние между отбираемыми единицами. Шаг отсчета определяется путем деления численности генеральной совокупности на численность выборочной совокупности .

Выбор начала отсчета рекомендуется производить путем случайного отбора из единиц первого интервала, т.е. первого шага отсчета. Например, производят проверку качества каждой 10-й, 20-й, 30-й и т.д.единицы произведенной продукции.

Механический отбор можно рассматривать как разновидность случайного бесповторного отбора, поэтому для оценки параметров генеральной совокупности при этом отборе применяются формулы случайной бесповторной выборки.

Выборки, при которых наблюдением охватывается небольшое число единиц (n<30), принято называть малыми выборками. Они применяются в тех случаях, когда невозможно или нецелесообразно использовать большую выборку. Например, при исследовании качества продукции, если это связанно с ее разрушением (при проверке на прочность, продолжительность срока службы и т.п.)

Предельная ошибка малой выборки определяется по формуле

Средняя ошибка , где 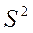- дисперсия малой выборки.

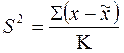,где

x – индивидуальные значения признака в малой выборке

- среднее значение признака в малой выборке

К – число степеней свободы К= n-1

Коэффициент доверия малой выборки t зависит не только от заданного уровня вероятности P, но и от численности единиц выборки.

Для определения коэффициента доверия t рассчитывают значение функции по формуле:

, где

p – уровень вероятности.

Затем определяют число степеней свободы К= n-1.

По таблице распределения Стьюдента в зависимости от значения функции и числа степеней К определяют значение t.

Рассмотрим определение генеральных характеристик при механическом отборе и малой выборке.

Задача

Из партии электроламп в 1000 штук произведена малая выборка каждой сотой лампы для определения их продолжительности службы.

Результаты выборки следующие:

№ лампы
Срок горения, час.

Определите: 1) доверительные интервалы, в которых заключена средняя продолжительность службы лампы для всей партии, гарантируя результат с вероятностью 0,97; 2) вероятность того, что средний срок службы ламп для всей партии отличается от полученного по выборке не более, чем на 48 часов.

Дата добавления: 2015-07-20