
Читайте также:
|
При простой случайной (собственно-случайной) выборке отбор единиц в выборочную совокупность производится непосредственно из всех единиц генеральной совокупности путем применения жеребьевки (лотереи) или путем использования таблиц случайных чисел, т.е. случайным образом. Данный отбор может быть проведен в форме повторной (возвратной) выборки и в форме бесповторной (безвозвратной).
Величина tm, обозначаемая D, называется предельной ошибкой выборки. Исходя из теорем П.Л. Чебышева и А.М. Ляпунова
Dx= tmx Dp= tmp, где
Dx – предельная ошибка выборки для средней
Dp – предельная ошибка для доли
mx – средняя ошибка для средней
mp – средняя ошибка для доли
t – коэффициент кратности средней ошибки выборки (доверия), зависящий от вероятности, с которой гарантируется величина предельной ошибки.
В зависимости от принятой вероятности Р определяется значение коэффициента доверия (t) по таблице удвоенной нормированной функции Лапласа.
Величины ошибок в условиях большой выборки рассчитываются по формулам, представленным в таблице 1.
Таблица 1 – Формулы ошибок простой случайной выборки и численности простой случайной выборки
| Способ отбора единиц | ||
| повторный | бесповторный | |
| Средняя ошибка m: для средней | mx= 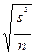
| 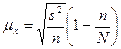
|
| для доли | 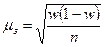
|  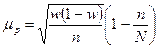
|
| Предельная ошибка D: для средней |

|
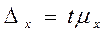
|
| для доли | Dp= tmp | Dp= tmp |
| Численность выборки n: для средней | 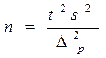
| 
|
| для доли | 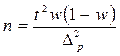
| 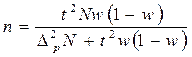
|
Формулы предельной ошибки позволяют решать следующие задачи:
1. Определение пределов генеральных характеристик (средней и доли) с заданной степенью вероятности на основе показателей полученных по данным выборки.
Дата добавления: 2015-07-20; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Протасовой О.В. | | | Доверительные интервалы (пределы) для генеральной средней |