Протасовой О.В.

Мичуринский государственный аграрный университет

Кафедра «Бухгалтерский учет, анализ и аудит»

Методические указания для самостоятельной работы

по статистике

Тема: «Выборочный метод»

Для студентов, обучающихся по специальности 080105 «Финансы и кредит»

УТВЕРЖДЕНО

методической комиссией

экономического факультета

протокол №

от «» 2008 г.

Мичуринск-Наукоград

Методические указания подготовлены ст.преподавателем

Протасовой О.В.

Рецензент: доцент кафедры экономики АПК Соколов О.В.

Рассмотрен на заседании кафедры статистики и анализа хозяйственной деятельности протокол №8 от 30 января 2008 г.

Рекомендован к изданию методической комиссией экономического факультета МГАУ (протокол № от «» 2008 г.)

СОДЕРЖАНИЕ

1. Понятие о выборочном наблюдении…………………………………………4

2. Простая случайная выборка…………………………………………………...7

3. Типологическая выборка…………………………………………………….15

4. Серийная выборка…………………………………………………………….19

5. Прочие способы формирования выборочной совокупности………………21

6. Контрольные вопросы и тесты……………………………………………….24

7. Задачи для самостоятельного решения……………………………………...27

Список рекомендуемых источников…………………………………………...34

1. Понятие о выборочном наблюдении

Выборочное наблюдение представляет собой такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, далее отобранная часть изучается, а затем результаты распространяются на всю исходную совокупность. Наблюдение осуществляется таким образом, что эта часть отобранных единиц представляет всю совокупность с достаточной для практике степенью точности.

Совокупность, из которой производится отбор, называется генеральной, и все ее обобщающие показатели – генеральными.

Выборочная совокупность – это совокупность единиц, отобранных из генеральной совокупности. Все ее обобщающие показатели называются выборочными.

Основными причинами, по которым во многих случаях выборочному наблюдению отдается предпочтение перед сплошным, являются:

1. экономия материальных, трудовых, финансовых ресурсов и времени в результате сокращения объема работы;

2. сведения к минимуму порчи или уничтожения исследуемых объектов;

3. необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц (например, при изучении бюджета домохозяйств);

4. достижение достаточно большой точности результатов обследования благодаря сокращению ошибок, происходящих при регистрации.

Преимущество выборочного наблюдения по сравнению со сплошным можно реализовать, если оно организовано и приведено в соответствии с научными принципами теории выборочного метода. Это обеспечение случайности, т. е. равной возможности попадания в выборку единиц генеральной совокупности, и достаточного числа единиц отбора.

Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (т.е. средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При этом следует иметь в виду, что при любых статистических исследованиях (сплошных и выборочных) возникают ошибки.

Ошибки регистрации могут возникать и при сплошных, и при выборочных наблюдениях. Они могут иметь случайный (непреднамеренный) и систематический (преднамеренный) характер.

Ошибки репрезентативности (представительности) присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенной с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборочных и генеральных характеристик.

Ошибки репрезентативности возникают вследствие двух причин:

1) из-за нарушения принципа случайности как основного принципа выборки (систематические ошибки)

2) в результате самого отбора (случайные ошибки)

Систематические ошибки выборки устраняются. Случайные ошибки устранить нельзя, но их рассчитывают и учитывают при переносе выборочных характеристик на генеральную совокупность.

Случайные ошибки репрезентативности бывают средними () и предельными ().

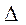Средняя ошибка выборки представляет собой такое расхождение между средними выборочной и генеральной совокупностей, которое не превышает среднеквадратическое отклонение в выборке.

Предельной ошибкой называется максимальное расхождение средних характеристик выборочной и генеральной совокупностей при заданной вероятности появления этой ошибки.

По методу отбора различают повторную и бесповторную выборки.

При повторной выборке ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами вновь попасть в выборку.

При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует.

По степени охвата единиц совокупности различают большие и малые (n < 30) выборки.

В практике выборочных исследований наибольшее распространение получили следующие виды выборки: простая случайная (собственно - случайная), механическая, типическая, серийная, комбинированная и др.

Основные характеристики параметров генеральной и выборочной совокупности обозначаются символами:

N – объем генеральной совокупности (количество единиц, входящих в генеральную совокупность)

n – объем выборочной совокупности (количество единиц, входящих в выборочную совокупность)

- генеральная средняя (среднее значение признака в генеральной совокупности)

- выборочная средняя (среднее значение признака в выборочной совокупности)

P – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности)

W – выборочная доля (доля, единиц обладающих данным признаком в выборочной совокупности)

- генеральная дисперсия (дисперсия признака в генеральной совокупности)

- выборочная дисперсия (дисперсия признака в выборочной совокупности)

t – коэффициент доверия при заданном уровне вероятности P

Дата добавления: 2015-07-20