
Читайте также:
|
Комбинированная выборка предполагает использование нескольких способов выборки. Можно комбинировать, например, серийную выборку и случайную. В этом случае, разбив генеральную совокупность на серии (группы) и отобрав нужное число серий, производят случайную выборку единиц в серии. Такая комбинированная выборка может быть повторной (для групп и единиц) и бесповторной.
Средняя ошибка комбинированной выборки определяется по формулам:
при повторном отборе - 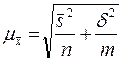 ;
;
при бесповторном отборе -  .
.
Многоступенчатая выборка предполагает извлечение из генеральной совокупности сначала укрупненных групп единиц, затем групп, меньших по объему, и так до тех пор, пока не будут отобраны те группы (серии) или отдельные единицы, которые будут подвергнуты наблюдению. Выборка может быть двухступенчатой, когда генеральная совокупность разбивается на группы и производится отбор групп, а затем внутри групп – отбор единиц наблюдения. На обеих ступенях отбор может вестись в случайном порядке.
При многофазной выборке выборочные совокупности образуются так, что одни сведения собираются от всех единиц отбора, затем отбираются еще некоторые единицы, которые и обследуются по более широкой программе. Расчет ошибки многофазной выборки производится для каждой фазы в отдельности.
Метод моментных наблюдений применяется для получения структуры затрат рабочего времени, характеристики использования оборудования. Сущность метода состоит в периодической фиксации состояния наблюдаемых единиц в заранее установленные или случайно выбранные моменты времени. При этом заранее составляется перечень всех возможных состояний процесса или видов затрат времени. По окончании наблюдения исследователь подсчитывает долю отметок о каждом состоянии или виде затрат времени в общем числе наблюдении; при этом считается, что доля времени, затраченного на данный вид работы, может быть оценена с помощью доли моментов, когда выполнялась эта работа, в общем числе наблюдений.
Средняя ошибка доли определяется по формуле простой случайной выборки:

где w – доля отметок о данном состоянии процесса;
n – количество моментов наблюдения.
Предельная ошибка Dp = tmp
Для определения численности моментов наблюдения применяется следующая формула:
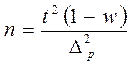
Доверительная вероятность и величина допустимой ошибки устанавливаются исследователем; величина w, как правило, неизвестна, поэтому обычно ориентируются на наибольшую дисперсию, когда w = 0,5[w(1-w) = 0.25].
После определения числа наблюдений устанавливается необходимое число обходов как частное от деления количества наблюдений на число рабочих мест, подлежащих обследованию.
Следующим этапом является составление графика проведения наблюдения. Наблюдение за состоянием процесса осуществляется через определенные промежутки времени. При моментном наблюдении со случайным отбором моменты отбираются при помощи таблиц случайных чисел. Второй способ целесообразен в тех случаях, когда наблюдение для объекта должно быть неожиданным.
Контрольные вопросы и тесты
1. Какие преимущества выборочного наблюдения делают его важнейшим источником статистической информации?
2. Какова сущность выборочного метода?
3. Каковы условия правильного отбора единиц совокупности при выборочном наблюдении?
4. Как классифицируются ошибки выборки?
5. При каком способе отбора ошибка выборки меньше? Почему?
6. Что представляет собой средняя ошибка выборки (для средней и доли)?
7. По каким формулам и зачем исчисляется предельная ошибка выборки (для средней и доли)?
8. Что показывает коэффициент доверия?
9. В чем особенность расчета случайных ошибок при малой выборке?
10. Назовите основные виды выборки.
11. Как производятся собственно-случайный и механический отборы?
12. Как производятся типический и серийный отборы?
13. Сущность комбинированного и многоступенчатого видов отбора.
14. Какие существуют способы оценки дисперсии в генеральной совокупности при определении необходимой численности выборки?
15. По каким формулам определяется необходимая численность выборки, обеспечивающая с определенной вероятностью заданную точность наблюдения?
16. Какая категория более широкая:
а) выборочное наблюдение
б) несплошное наблюдение
17. Какие ошибки могут возникать при выборочном наблюдении:
а) случайные ошибки регистрации
б) систематические ошибки регистрации
в) случайные ошибки репрезентативности
г) систематические ошибки репрезентативности
18. Между ошибками выборки и объемом выборочной совокупности существует:
а) прямая зависимость
б) обратная зависимость
в) зависимости нет
19. Предельная ошибка при уровне вероятности, превышающем 0,7:
а) меньше средней ошибки выборки
б) больше средней ошибки выборки
в) равна средней ошибки выборки
г) не зависит от средней ошибки выборки
20. Какая выборка может быть реализована только на основе бесповторного отбора:
а) собственно – случайная
б) механическая
в) типическая
г) серийная
21. Какой отбор при прочих условиях обеспечивает меньшую необходимую численность выборки:
а) повторный
б) бесповторный
22. Средняя ошибка типической выборки при обоснованной типизации генеральной совокупности:
а) меньше средней ошибки собственно – случайно выборки
б) равна средней ошибке собственно – случайной выборки
в) больше средней ошибки собственно – случайной выборки
23. Какие единицы обследуются внутри групп при серийном отборе:
а) все единицы
б) отобранные собственно – случайным способом
в) отобранные механическим способом
24. Какие единицы обследуются внутри групп при типическом отборе:
а) все единицы
б) отобранные собственно – случайным способом
в) отобранные механическим способом
25. Для каких способов формирования выборочной совокупности необходимый объем выборки определяется по одним и тем же формулам:
а) собственно – случайного и механического
б) собственно – случайного и типического
в) собственно – случайного и серийного
г) типического и серийного
26. Из перечисленных отмечать способы (методы) отбора единиц из генеральной совокупности в выборочную:
а) типической
б) собственно – случайным
в) механический
г) повторный
д) бесповторный
27. Проведено собственно – случайное бесповторное обследование заработной платы сотрудников 2-х фирм. Обследовано одинаковое число сотрудников. Дисперсия зарплаты для 2-х фирм одинаковая, а численность сотрудников дольше на 1-ой фирме. Средняя ошибка выборки:
а) больше на 1-ой фирме
б) больше на 2-ой фирме
в) на обеих фирмах одинаковая
28. Если степень вероятности 0,997, то значение коэффициента доверия равно:
а) 1
б) 2
в) 3
г) 99,7%
29. Если уменьшить численность случайной повторной выборки в 4 раза, то средняя ошибка выборки:
а) уменьшится в 2 раза
б) увеличится в 2 раза
в) увеличится в 16 раз
г) уменьшится 4 раза
30. Степень вероятности изменяется с 0,997 до 0,954. Предельная ошибка при неизменности прочих факторов:
а) увеличится
б) уменьшится
в) не изменится
Дата добавления: 2015-07-20; просмотров: 159 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Серийная выборка | | | Задача 15 |