Многоразрядные сумматоры

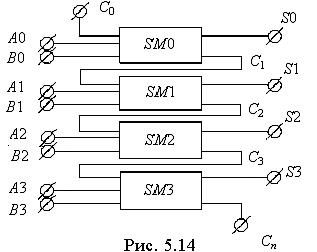
Для суммирования многоразрядных двоичных чисел используются многоразрядные сумматоры, которые строятся на основе одноразрядных сумматоров. Простейшая структура четырехразрядного (n = 4) двоичного сумматора с последовательным переносом приведена на рис. 5.14. В этой схеме два четырехразрядных двоичных числа А 0, А 1, …, А 3, В 0, …, В 3 суммируются поразрядно (разряд А 0 с разрядом В 0, А 1 с В 1, А 2 с В 2, А 3 с В 3) одноразрядными полными сумматорами SM 0, …, SM 3. Разряды сумматора связаны между собой цепями внутреннего переноса С ₁, С ₂, С ₃, по которым передаются сигналы переноса из младшего разряда в старший.

Разряды двоичных чисел суммируются параллельно (одновременно), но сигналы переноса С ₁, …, С_n передаются последовательно от нулевого разряда (С ₁) до внешнего выхода (С_n). Такой перенос называют последовательным переносом. При этом время задержки t _задсигнала при последовательном переносе от SM 0 до внешнего выхода С_n получается большим:

t _зад = n × t _с, (5.15)

где t _с – задержка сигнала переноса одном разряде.

Суммирование заканчивается появлением сигнала переноса на внешнем выходе С_n.

При большом числе разрядов (n > 4, …, 8) время задержки t _зад оказывается настолько большим, что применение сумматоров с последовательным переносом становится невыгодным. Для уменьшения t _зад в быстродействующие многоразрядные сумматоры вводятся схемы ускоренного переноса (СУП). При наличии СУП сигналы переноса в каждом разряде (в том числе и С_n) формируются одновременно с формированием суммы.

Для формирования сигнала переноса одновременно с суммой в i -м разряде надо учитывать все сигналы предыдущих разрядов, т.е. все те сигналы, которые использовались для формирования сигналов внутреннего переноса в предыдущих разрядах. Для упрощения логических выражений и схемы вводят вспомогательные функции [3]

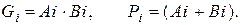(5.16)

Тогда вместо (5.12) получаем выражение [3]:

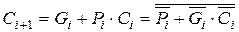. (5.17)

Функции 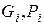формируются на входах каждого разряда и используются далее вместо входных сигналов Ai, Bi. По этому правилу построен четырёхразрядный сумматор с СУП, фрагмент которого приведен на рис. 5.15 (разряды 0,1).

Вспомогательные функции 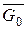, 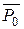формируются вентилями В1, В2, 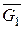, 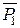– вентилями В3, В4. Суммы S 0, S 1формируются так же, как в схеме на рис. 5.13,а. Только промежуточные суммы S 0¢, S 1¢ формируются не из входных сигналов Ai, Bi, а из вспомогательных функций G_i, P_i. Например,

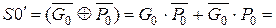
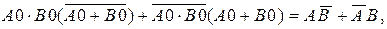= (5.18)

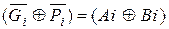. (5.19)

При получении (5.18) использованы теоремы де Моргана: 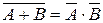, 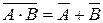. Сигналы переноса С ₁, С ₂ формируются схемами И-ИЛИ-НЕ (вентили В5, В6) в соответствии с (5.17):

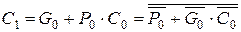, (5.20)

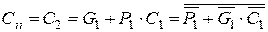. (5.21)

Так, 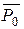поступает на схему ИЛИ-НЕ (В5) через вентиль В5.2 с выхода вен-тиля В2. Сигналы 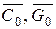перемножаются вентилями В5.1 и В6.2, произве-дение 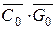поступает на схему ИЛИ-НЕ (В5). Точно так же формируется сигнал С ₂ в разряде 1.

Чтобы сформировать выходной сигнал переноса С ₂, на схему форми-рования сигнала переноса в последнем (n – 1) разряде (вентиль В6) подают-ся вспомогательные логические сигналы (функции) 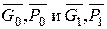, вследствие чего сигнал C_n формируется одновременно с сигналом С ₁. Схема сумматора при этом стала сложнее, чем при последовательном переносе. Сумматоры с СУП, имеющие больше разрядов (n = 4), действуют точно так же, как рассмотренный двухразрядный. Однако сложность логической функции (5.17), (5.21) и схемы формирования сигнала переноса C _i+1 быстро возрастает с увеличением i. Поэтому данный способ используется при i £ 4[3]. По рассмотренному принципу формирования ускоренного переноса построены четырехразрядные быстродействующие сумматоры К155ИМ3, К555ИМ6. Время задержки сигнала переноса от входа С ₀ до C_n микросхемы К155ИМ6 не превышает 17 нс (t _зад £ 17 нс), а время формирования суммы t_S £ 24 нс.

При построении в одной СИС (БИС) многоразрядных сумматоров (n = 8, 16, …) разряды объединяются в группы из двух или четырех разрядов. Внутри групп и между ними могут использоваться ускоренный (для быстродействующих сумматоров) или последовательный (для медленнодействующих) переносы [3]. Для ускоренного переноса между группами в них вырабатываются специальные функции X, Y – аналоги функции 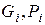в группах.

В многоразрядные сумматоры объединяются также микросхемы четырехразрядных сумматоров с СУП. Для ускоренного переноса между микросхемами четырехразрядных сумматоров в них (как в группах) вырабатываются специальные функции переноса X, Y. Для организации ускоренного переноса между микросхемами четырехразрядных сумматоров выпускаются специальные СИС, например К155ИП4, с помощью которой можно организовать ускоренный перенос между четырьмя микросхемами четырехразрядных сумматоров [5].

Арифметико-логическое устройство (АЛУ). Так называют функциональный блок, который выполняет заданный набор арифметических и логических функций над двумя многоразрядными операндами (словами). В состав арифметических операций входит обязательно суммирование (сложение и вычитание). Часто АЛУ производит сдвиг двоичных чисел влево и вправо. При суммировании применяется СУП.

В состав логических функций обычно входят все логические функции двух переменных (табл. П1). АЛУ значительно сложнее сумматоров. Например, для реализации четырехразрядного АЛУ используется около 70 логических элементов И-НЕ либо ИЛИ-НЕ [3].

Дата добавления: 2015-07-25