Полный сумматор (SM)

Слагаемыми при суммировании, как правило, являются многоразрядные числа А (А 0, А 1, …, А_{n -1}), В (В 0, В 1, …, В_{n -1}). Сумматор при этом суммирует два i -x разряда (Ai + Bi). По правилу (5.9), (5.10) суммируются все разряды чисел А и В, в том числе и младший Ai -1, Bi -1. Теперь при сложении i -x разрядов Ai, Bi нужно учитывать возможность образования переноса C_i из младшего (i – 1) разряда в i -й разряд. Эта единица переноса C_i должна учитываться при суммировании в i -м разряде вместе с Ai, Bi. Таким образом, при суммировании i -х разрядов чисел (Ai, Bi) нужно суммировать уже три двоичных разряда Ai, Bi, C_i и формировать единицу переноса в старший (i + 1) разряд – C_{i +1}. Устройство, которое выполняет эти функции, называют полным сумматором.

Алгебраические выражения, полученные из таблицы истинности, для Si и переноса C_{i +1} могут быть представлены в виде [3]

(5.11)

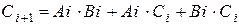. (5.12)

Таблица истинности полного сумматора представлена табл. 5.16.

Таблица 5.16

i	Входы	Выходы	Десятичный эквивалент
Сi	Ai	Bi	Si	Ci +1

Выражение (5.11) – это неминимизированная СДНФ; (5.12) – это МДНФ (см. приложение). Сумма (5.11) совпадает с логической функцией Исключающее ИЛИ (И.ИЛИ) над тремя логическими переменными Ai, Bi, C_i, поэтому ее удобно реализовать при помощи двух логических элементов И.ИЛИ. Вариант схемы полного сумматора на двух логических элементах И.ИЛИ (В1, В2) приведен на рис. 5.13,а, условное обозначение показано на рис. 5.13,в.

Вентили В1, В4 образуют первый полусумматор (см. рис. 5.12,а), осуществляющий суммирование двух чисел Ai, Bi, образуя при этом промежуточную сумму и инверсный сигнал переноса (тоже промежуточный) . Второй полусумматор (вентили В2, В3)

б

в

Рис. 5.13

осуществляет сложение промежуточной суммы и сигнала переноса C_i (от младшего разряда), образуя полную сумму Si и инверсный сигнал переноса (второй промежуточный). Вентиль В5 формирует сигнал переноса 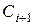в старший разряд из промежуточных сигналов , :

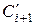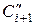С_{i+ 1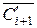} = = + . (5.13)

Следует отметить, что комбинация сигналов C'_{i+ 1}= 0, 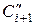= 0 не реализуется: если Ai = Bi = 1, то С'_{i+ 1} = 0, 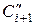= 1 (так как = 0). Во всех остальных случаях С'_{i+ 1}=1.

Алгебраическое выражение для суммы Si остается без изменения (5.11). Алгебраическое выражение для C_{i +1} получим после подстановки значени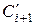й и 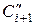в (5.13):

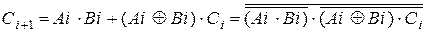. (5.13,а)

Последнее выражение в (5.13,а) подготовлено для реализации на базовых элементах И-НЕ (см. приложение).

Полный сумматор может быть реализован на других ЛЭ (И-НЕ, ИЛИ-НЕ и др.). На рис. 5.13,б приведен один из вариантов сумматора (вариант МДНФ) на базовых элементах И-НЕ. Вентили В1, …, В4 образуют эквивалент И.ИЛИ1 исключающего ИЛИ (эквивалент вентиля В1 на рис. 5.13,а), а вентили В5, …, В8 – эквивалент И.ИЛИ2 (эквивалент вентиля В2 на рис. 5.13,а). Алгебраическое выражение функции () исключающего ИЛИ (И.ИЛИ1), реализованного на ЛЭ И-НЕ, имеет вид (см. приложение)

. (5.14)

Сигнал 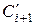образуется на выходе вентиля В1 (внутри И.ИЛИ1), а сигнал 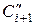на выходе В5 (внутри И.ИЛИ2). Поэтому отдельных вентилей (В3, В4 на рис. 5.13,а) для формирования сигналов 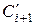, 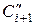нет. Вентиль В9 выполняет ту же функцию, что и В5 на рис. 5.13,а.

Дата добавления: 2015-07-25