Линейные токи

Читайте также:

В большинстве практически важных случаев постоянные токи текут по проводам, распределяясь с равномерной плотностью по сечению провода. Такие токи называют линейными.

Рассмотрим элемент dl проводника. Его объем: , тогда

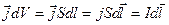
Тогда закон БСЛ:

Поле элементарных токов

Замкнутые токи, текущие в области, линейные размеры которой << расстояния до точек, в котором вычисляется магнитное поле.

Рассмотрим поле элементарного тока. Его вектор-потенциал . Т.к. ток электрический, то

Тогда

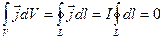Т.к.

Приставим слева -справа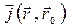

Интеграл

Для доказательства умножим его на произвольный вектор :

На поверхности, ограничивающей объём

, т.к. - любой вектор, то

При интегрировании постоянно, тогда

Вектор - магнитный момент элементарного тока

Тогда

Магнитное поле замкнутого проводника убывает обратно пропорц. кубу расстояния.

Магнетика в магнитостатическом поле

В результате помещения неолита во внешнее магнитное поле они приобретают?????(намагничиваются).

Магнитный момент единого объёма магнетика

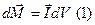I – вектор намагничивания.

Диамагнетик – дополнительное поле, по направлению противоположное первоначальному;

Парамагнетик – в ту же сторону;

Ферромагнетик.

Величина вектора намагничивания связана с первоначальным внесением магнитного поля:

- коэффициент магнитной восприимчивости.

Векторный потенциал при наличии поля

Магнитное поле определяется полем токов проводимости 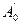и полем, которое возникает за счет намагничивания магнетика

(2) показывает что претерпевает разрыв, поэтому необходимо выделить поверхность разрыва.

Считая что положительная нормаль к поверхности S направлена в сторону магнетика (2) учитывая S’ к S, получим

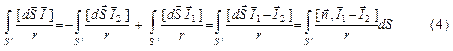
Если считать что все магнетики расположены внутри рассматриваемого объема V так, что поверхность S’’ не пересекает магнетики, то в первом интеграле (3)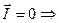

Второй интеграл преобразуется по (4), тогда

S – сумма всех поверхностей разрыва .

Магнитных зарядов не существует магнитное поле может быть вызвано только токами. Эти токи связывают с движением зарядов в молекулах.

Из сравнения и видно, что роль объемной плотности тока играет ;

Средняя объемная плотность молекулярных токов

Связь магнитной проницаемости и магнитной восприимчивости.

В присутствии магнетика необходимо учитывать поле, созданное молекулярными токами.

Поле, созданное токами проводимости: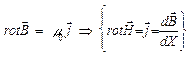

Чтобы учесть наличие магнетика:

С другой стороны, уравнение Максвелла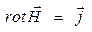

Справедливо как при наличии магнетиков, так и при их отсутствии, то есть

Подставим в (5)

Энергия магнитного поля постоянных токов

Из общего выражения для электромагнитного поля вытекает

Т.е. энергия магнитного поля распределяется в пространстве с плотностью

Т.е.

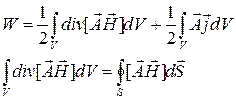
Если все токи расположены в конечной области пространства, то

Т.е. на больших расстояниях подынтегральное выражение убывает, как . Поскольку поверхность интегрирования растёт как , то интеграл при убывает, как . поэтому при удалении S на бесконечность интеграл , т.е.

Энергия магнитного поля как энергия взаимодействия тока с магнитным полем, характеризируемым потенциалом .

Если потенциал заменить выражением 6 через токи

то

где – расстояние между элементами объёма dV и dV’.

Интегрирование (5) сводится к интегрированию по объёму проводников. Поэтому обозначая через Vk объём k-го проводника

Где - плотность тока текущего по j-му и k-му проводнику, rik- расстояние между элементами объёма dVi и dVj соответствующих проводников.

Формулировку можно переписать в следующем виде:

Коэффициенты

зависят только от формы проводника и не зависят от силы тока, протекающего по проводникам.

(6) можно использовать для вычисления коэффициента самоиндукции проводника. Для одного изолированного проводника (6):

Если имеется возможность определить W, то из этой формулы м.б. найдена величина L.

В случае линейных токов

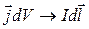
Т.е. коэффициенты взаимной индукции (7)

- формула Неймана

-контуры i-го и k-го контуров с током.

Из формул (7) и (8) следует, что

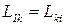
Определить магнитный момент линейного тока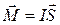

1) Найти векторный потенциал и магнитное поле шара радиуса R, равномерно заряженного по объёму зарядом Q и вращающегося с постоянной скоростью и вокруг оси, проходящей через центр, на расстоянии r>>R.