Читайте также:
|
магн.в-ра, 
эл.в-ра
Стационарное – не зависящее от времени, нестационарное (переменное) – зависящее от времени
1. 
, Ф 
магн. потоки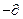 
Ф/ 
· Смысл: источником эл. поля (слева в-р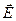 
) является переменное маг. поле (справа 
); ур-е э-м индукции Фарадея
2. 
, 
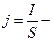плотн. тока проводимости, 
вект. плотн. «тока» смещения
· Смысл: источником маг. поля (слева в-р 
) являются токи проводимости (справа 
) и переменное эл. поле (справа «токи» смещения)
3. 
, 
своб. эл. заряд; заряж. тело
· Смысл: теорема Остроградского – Гаусса для эл. поля в среде; источником эл. поля в среде (слева в-р 
) являются эл. заряды (справа 
)
4. 
· Смысл: теорема Остроградского – Гаусса для маг. поля в среде; отсутствие маг. зарядов
Поэтому если:
Только нет справа есть эл. поле, но в отсутствии зарядов или заряженных тел
Только нет справа 
есть только стационарное эл. поле
Нет того и другого – вообще нет электрического поля
Только нет справа 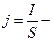есть магн. поле, но в отсутствии токов проводимости
Только нетсправа 
есть только стационарное маг. поле
Нет того и другого – вообще нет магнитного поля
(Иногда в вариантах ответа называют чего нет, а иногда – что есть.)
Любое скалярное произведение в-ров имеет вид:
, 
, 
, 
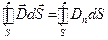Дата добавления: 2015-07-25; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Полная система уравнений Максвелла | | | Линейные токи |