Выпуклость графика функции. Точки перегиба

График функции называется выпуклым вверх (вниз) на некотором промежутке, если он расположен ниже (выше) касательной, проведенной к графику функции в любой точке этого промежутка.

Достаточное условие выпуклости графика функции. Пусть функция , имеет первую и вторую производные. Тогда если для всех , то на этом интервале график функции выпуклый вверх, если же для всех , то на этом интервале график функции выпуклый вниз.

Точкой перегиба графика функции называется такая его точка, которая отделяет участок выпуклости вверх от участка выпуклости вниз. Необходимое условие существования точки перегиба графика функции. Если - точка перегиба графика функции , то или не существует. Достаточное условие существования точки перегиба графика функции. Если при переходе через точку меняет знак, то точка является точкой перегиба графика функции f.

Алгоритм нахождения интервалов выпуклости и точек перегиба графика функции:

1) найти ; 2) решить уравнение = 0 и найти точки, в которых не существует;

3) полученные точки нанести на числовую ось и найти на каждом из полученных интервалов знак ;

4) если >0, то на этом интервале график функции выпуклый вниз, <0 – выпуклый вверх;

5) если при переходе через точку меняется знак , то точка с абсциссой 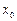является точкой перегиба графика функции.

Дата добавления: 2015-07-25