
Читайте также:
|
Достаточный признак возрастания функции  : если
: если 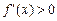 в каждой точке некоторого интервала, то
в каждой точке некоторого интервала, то  возрастает на этом интервале. Достаточный признак убывания функции
возрастает на этом интервале. Достаточный признак убывания функции  : если
: если  в каждой точке некоторого интервала, то на этом интервале функция убывает. Следовательно, отыскание промежутков монотонности функции
в каждой точке некоторого интервала, то на этом интервале функция убывает. Следовательно, отыскание промежутков монотонности функции 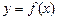 сводится к нахождению промежутков знако-постоянства ее первой производной
сводится к нахождению промежутков знако-постоянства ее первой производной 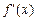 .
.
Точка х = х 0 называется точкой максимума (минимума) функции 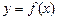 , если существует такая окрестность точки х 0, что для всех х (х
, если существует такая окрестность точки х 0, что для всех х (х 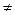 х 0) из этой окрестности выполняется неравенство
х 0) из этой окрестности выполняется неравенство  <
< 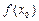 (соответственно
(соответственно  >
> 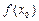 ). Точки максимума и минимума функции называются точками ее экстремума, а значения функции в точке максимума (минимума) – максимумом (минимумом) или экстремумом функции. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции. Не всякая критическая точка является точкой экстремума.
). Точки максимума и минимума функции называются точками ее экстремума, а значения функции в точке максимума (минимума) – максимумом (минимумом) или экстремумом функции. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции. Не всякая критическая точка является точкой экстремума.
Теорема Ферма (необходимое условие экстремума). Если точка х 0 является точкой экстремума функции f и в этой точке существует производная 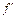 , то она равна нулю
, то она равна нулю 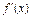 =0.
=0.
Достаточное условие существования экстремума: Пусть функция  непрерывна в точке х 0 и имеет производную в некоторой окрестности точки х 0, кроме, может быть, самой точки х 0, тогда:а) если
непрерывна в точке х 0 и имеет производную в некоторой окрестности точки х 0, кроме, может быть, самой точки х 0, тогда:а) если 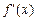 при переходе через точку х 0 меняет знак с плюса на минус, то точка х 0 является точкой максимума функции
при переходе через точку х 0 меняет знак с плюса на минус, то точка х 0 является точкой максимума функции  ;
;
б) если 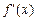 при переходе через точку х 0 меняет знак с минуса на плюс, то точка х 0 является точкой минимума функции
при переходе через точку х 0 меняет знак с минуса на плюс, то точка х 0 является точкой минимума функции  .
.
Алгоритм нахождения промежутков монотонности и точек экстремума:
1) найти критические точки функции f и нанести их на числовую прямую, выделив точки разрыва функции f;
2) найти знак производной на каждом из получившихся промежутков;
3) определить по знаку производной характер монотонности функции на каждом промежутке;
4) выяснить наличие экстремума в каждой критической точке, отличной от точек разрыва функции.
Дата добавления: 2015-07-25; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| С невестами туго, ну что тут сказать…. | | | Выпуклость графика функции. Точки перегиба |