Основные квантово-механические механизмы взаимодействия оптического излучения с атомами и молекулами

Внутренняя энергия атомов и молекул складывается из энергии электронов, находящихся в электростатическом взаимодействии с ядрами, энергии колебания самих ядер относительно друг друга и энергии вращения молекулы (атома) как целого.

Поскольку электрон может рассматриваться не только как частица, но и как волна, для расчета его энергии в молекулах может применяться уравнение Шредингера, количественно описывающее свойства стоячих волн в модели так называемого потенциального ящика. Заметим, что данное уравнение постулировано, а не выведено. Однако в настоящее время многочисленные экспериментальные данные позволяют считать его верным.

В упрощенном виде для стационарного случая уравнение Шредингера выглядит следующим образом:

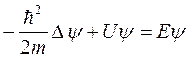…(7)

После замены 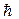на h (h = 2p 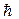) получим:

(8)

В уравнении (8) y - так называемая волновая функция (пси-функция), описывающая электромагнитные возмущения в системе; D - оператор Лапласа, представляющий собой сумму вторых частных производных от стоящей за ним величины по всем 3 пространственным направлениям. Иными словами:

(9)

Е – полная, а U – потенциальная энергии частицы, m – её масса (электрон, в отличие от фотона, обладает массой покоя).

Уравнение Шредингера является дифференциальным уравнением второго порядка, решение которых не всегда возможно и является сложной математической задачей. Тем не менее, известны решения этого уравнения для одномерного случая (электронные волны в потенциальном ящике одномерны) и для атома водорода. Мы приведем здесь только одно решение – для модели одномерного потенциального ящика:

(10)

Квадрат модуля волновой функции |y|² соответствует вероятности пребывания электрона в данной точке (или вблизи нее), величина y₀ – амплитуда изменения волновой функции, l – длина (размер) потенциального ящика, а n принято называть главным квантовым числом. Оно принимает только целочисленные значения – 1, 2, 3 и т.д. Из полученного решения (уравнение (10)) вытекает, что из-за своих волновых свойств электроны обязаны пребывать на определенных орбиталях (уровнях), соответствующих местам формирования стоячих волн в молекуле (рассматриваемой как «потенциальный ящик») вследствие интерференции. Каждой такой орбитали (уровню) соответствует определенное значение энергии электрона, пропорциональное n²:

(11)

где Е_е – энергия электрона, а m – его масса.

Что касается расчета распределения электронных плотностей в реальных атомах, то из-за своей сложности, как уже указывалось выше, он был произведен только для атома водорода. Для более крупных атомов или многоатомных молекул расчет затруднен в связи с тем, что в трехмерном пространстве стоячие электронные волны будут формироваться в трех измерениях, и для их характеристики требуются, как минимум, три квантовых числа. Тем читателям, которые хотят более подробно ознакомиться с квантово-механическими принципами расчетов электронных орбиталей, можно рекомендовать обратиться к специальным учебникам по квантовой химии и физике.

На основании приведенных выше квантово-механических уравнений можно сделать следующие заключения:

1. Электроны в покоящихся стабильных атомах и молекулах пребывают на определенных электронных орбиталях, каждая из которых соответствует конкретному набору квантовых чисел.
2. Изменение энергии электрона в составе атома или молекулы неизбежно должно привести к изменению его орбитали (энергетического уровня).
3. Переход электрона при изменении его энергии происходит только дискретно (квантовано), т.е. с одной орбитали на другую.
4. Межорбитальный переход электрона становится возможен только в тех случаях, когда энергия электрона меняется на величину, соответствующую различиям в энергии у ранее занимавшейся им орбитали и орбитали, на которую электрон переходит.

В каждом типе молекул имеется набор занятых и свободных электронных орбиталей (электронных уровней). Величина энергий, необходимых для электронных переходов между этими орбиталями, определяется структурой молекулы, вследствие чего для каждого типа молекул набор этих энергий уникален и может служить своеобразным «отпечатком пальца» этого соединения. Следует, впрочем, заметить, что обычно молекулы находятся в окружении других молекул (например, молекул растворителя) и взаимодействуют с ними тем или иным образом. Такое взаимодействие может повлиять на энергии занятых и свободных электронных орбиталей. Иногда это влияние бывает достаточно сильно.

Как следует из табл. 1, энергии квантов излучения, приходящегося на оптический спектральный диапазон, позволяют им взаимодействовать преимущественно с электронными оболочками атомов и молекул.

Электроны в молекулах принято разделять на три группы. Это:

• n -электроны, не участвующие в образовании ковалентных межатомных связей в молекулах;
• s -электроны, участвующие в образовании прочных одинарных s -связей;
• р -электроны, участвующие в образовании менее прочных, двойных или тройных p -связей.

Указанные типы электронов в молекулах располагаются соответственно на n -; s- и p - молекулярных электронных орбиталях. Заметим, что электроны на s- и p - молекулярных орбиталях, формирующих ковалентные связи между составляющими молекулами атомами, обобщены и не являются «собственностью» какого-либо из атомных ядер данной молекулы.

Кванты излучения могут взаимодействовать с электронами любого типа, однако для возбуждения n- и s -электронов требуются значительные энергии, поэтому на них оказывают влияние только кванты с малой длиной волны (т.е. большой энергией), входящие в так называемый вакуумный ультрафиолетовый спектральный поддиапазон.

Следствием взаимодействия кванта с электроном является увеличение энергии последнего на величину, соответствующую энергии поглощенного кванта излучения. Из приводившихся выше квантово-механических моделей следует, что изменение энергии электрона с неизбежностью приводит к тому, что он оказывается вынужден изменить свою орбиталь в молекуле, заняв ту из них, которая соответствует новому значению его энергии (см уравнение (11)). Вместе с тем, для такого перехода электрону требуется совершенно определенная порция энергии, соответствующая разнице в этом показателе между «старой» и «новой» орбиталями (орбитали квантованы, каждая из них соответствует определенным значениям квантовых чисел, которые могут быть только целыми). Поэтому электроны молекул взаимодействуют не с любыми квантами, а только с теми из них, энергия которых удовлетворяет вышеуказанному требованию. Кванты же, не удовлетворяющие ему, взаимодействовать с электронами данной молекулы не будут.

На практике это означает, что взаимодействие квантов излучения оптического спектрального диапазона с молекулами будет различным у фотонов с разной длиной волны (частотой, волновым числом). Излучение с «подходящими» по энергии (или, что то же самое, по l, v или n) квантами будет при прохождении через содержащий конкретные молекулы объект ослабляться сильно, а с «неподходящими» - слабо (может даже проходить через объект совсем без ослабления). Напомним, что у каждого типа молекул – свой набор электронных орбиталей, различающихся по энергиям, определяющийся структурой молекул данного типа. Поэтому каждый определенный тип молекул будет ослаблять излучения с определенными l, v и n. Это обстоятельство позволяет решать с помощью оценки ослабления образцом излучения с разными l (v или n) качественные задачи, т.е. выявлять присутствие в объекте конкретных химических соединений.

Рассмотрим теперь, что происходит с электронами в молекулах после поглощения квантов электромагнитного излучения оптического спектрального диапазона.

Дата добавления: 2015-07-25