Количественное описание поглощения света растворами. Закон Бугера-Ламберта-Бера.

При исследовании прохождения монохроматического излучения через растворы способных к его поглощению соединений (хромофоров) выявляется зависимость ослабления света в образце от концентрации молекул-хромофоров в растворе. Выведем эту зависимость. Для этого рассмотрим следующую модель (рис 2.): пусть имеется объект (например, кювета с раствором) плоско-параллельной формы (передняя, обращенная к источнику излучения, и задняя поверхности объекта являются параллельными друг другу плоскостями) с толщиной l. На переднюю стенку этого объекта падает параллельный пучок монохроматического излучения с интенсивностью J₀, а через его заднюю стенку выходит непоглощенное излучение с интенсивностью J. Концентрация хромофорных молекул в объекте пусть составляет n молекул/см³, а поперечное сечение каждой молекулы в плоскости, перпендикулярной направлению освещения объекта, обозначим как r.

Рисунок 2. Схема, иллюстрирующая вывод закона Бугера-Ламберта-Бера. Кружками на схеме обозначены поглощающие свет молекулы. Остальные пояснения в тексте.

Будет считать, что квант излучения, попавший в площадь r каждой молекулы, поглощается ею и далее не существует. Выберем на расстоянии х от передней стенки объекта тонкий слой толщиной dx. На него будет попадать уже ослабленное излучение с интенсивностью J^¢. Определим, насколько ослабится J^¢ после прохождения слоя dx. Легко понять, что это ослабление (dJ^¢) будет зависеть от относительной суммарной площади поперечного сечения всех молекул-хромофоров, попавших в объем толщиной dх, т.е. доли всей освещенной площади (S_осв) образца, затеняемой молекулами в этом слое. При общей концентрации данных молекул в образце n молекул/см³ эта относительная суммарная площадь будет равна:

где S_отн – относительная затеняемая молекулами в слое толщиной dx площадь, а S_осв – общая освещенная площадь объекта.

Ослабление же света d J^¢ в слое dx будет равно:

(12)

Полученное уравнение (12) является простейшим дифференциальным уравнением с разделяющимися переменными. Решим его:

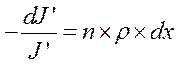
(13)

(14)

Уравнение (14) носит название закона Бугера-Ламберта-Бера. Он количественно описывает зависимость снижения интенсивности монохроматического света от концентрации n поглощающих свет молекул в объекте. Величина r, входящая в уравнение (14), носит название поперечного сечения поглощения молекулы. Она специфична для каждого из хромофоров и, кроме того, зависит от длины волны (энергии квантов, частоты или волнового числа) излучения, ослабление которого измеряется. Размерность r - см²/молекулу. Величина l в этом же уравнении называется оптическим путем. Это расстояние, которое проходят кванты излучения в веществе образца. В большинстве случаев оптический путь равен внутренней толщине кюветы, в которой находится образец, но имеются и исключения, которые будут рассмотрены ниже. Поскольку освещенная площадь объекта (S_осв) при измерениях не меняется, можно заменить значения интенсивностей в формуле (14) на соответствующие значения потоков:

(15)

На практике, однако, закон Бугера-Ламберта-Бера обычно применяют в другой форме. Связано это с тем, что концентрации веществ-хромофоров редко выражаются в количестве молекул в см³ образца. Кроме того, удобно ввести показатель, который зависел бы от концентрации хромофора линейно. Для этого обе части уравнения (15) можно разделить на F_о, а затем прологарифмировать.

(16)

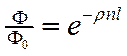
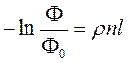
Из уравнения (16) видно, что величина зависит от концентрации хромофора n линейно.

Если же желательно, чтобы концентрация вещества была выражена в моль/л, тогда применяется иная форма уравнения (16):

(17)

В уравнении (17) концентрация хромофора с выражена уже в моль/л. Показатель же e, заменяющий в выражении (17) r, носит название молярного коэффициента поглощения. Его размерность – л/(моль×см). Численно величина e составляет 2,62´10²⁰ r (а r = 3,8´10^-21 e). Поскольку r зависит от длины волны (частоты, энергии квантов, волнового числа) излучения, при которой проводятся измерения, ясно, что и величина e также будет зависеть от этих показателей.

Из уравнения (17) вытекает, что от молярной концентрации хромафора в исследуемом объекте (с) линейно зависит отрицательный десятичный логарифм отношения потоков выходящего из объекта и падающего на него излучения (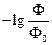). Поэтому эта величина получила специальное название – оптическая плотность. Она обычно обозначается буквой D.

Определение 10:

Оптической плотностью объекта D называется отрицательный десятичный логарифм отношения потоков или интенсивностей вышедшего из него и попавшего на него излучения.

(18)

Подставив величину D в уравнение (17), получим ту форму закона Бугера-Ламберта-Бера, которая чаще всего и используется в фотометрическом анализе на практике:

(19)

Из уравнения (19) становится понятен физический смысл молярного коэффициента поглощения.

Определение 11:

Молярным коэффициентом поглощения называется оптическая плотность D при данной длине волны (энергии фотонов, частоте, волновом числе) излучения образца хромофора с концентрацией 1 моль/л и с длиной оптического пути 1 см.

Отношение величин интенсивностей (или потоков) вышедшего из объекта и попавшего в объект света (J/J₀ или F/F₀) принято называть светопропусканием объекта. Иногда, впрочем, эту величину также называют и просто пропусканием. Стандартное обозначение светопропускание – Т. Хотя по своему смыслу Т – величина безразмерная, ее обычно выражают в %. Из приведенного выше уравнения (18) ясно, что и оптическая плотность D также является величиной безразмерной. Нужно хорошо помнить все соотношения, связывающие между собой величины D и Т, поскольку в спектрофотометрических расчетах часто приходится переходить от D к Т, и обратно.

(20)

(21)

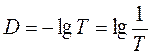
Из уравнения (21) видно, что Т, в отличие от D, от концентрации хромофора в объекте зависит нелинейно.

Иногда для характеристики ослабления излучения в образце применяется также показатель 1 – Т. Этот показатель носит название поглощение. Далее, при необходимости применения такого показателя, будем обозначать его В. Из сказанного вытекает, что:

(22)

Видно, что В, как и Т, от концентрации хромофора в образце зависит нелинейно.

Следует заметить, что в отсутствие образования комплексов между молекулами-хромофорами в объекте каждая из них поглощает свет независимо от других. Поэтому в сложных по своему составу объектах, содержащих несколько типов хромофорных молекул, общая оптическая плотность образца (D_обр) будет простой суммой оптических плотностей, определяемых поглощением излучения каждым из хромофоров:

(23)

К сожалению, в биологических объектах молекулы-хромофоры часто образуют устойчивые комплексы с другими молекулами и друг с другом за счет нековалентных взаимодействий (водородных связей, электростатического взаимодействия и т.д.). При образовании такого комплекса получается новый хромофор, величина e которого при длине волны измерения может отличаться от таковых у формирующих этот комплекс молекул. В таких случаях уравнение (23) не выполняется.

Дата добавления: 2015-07-25