Вычисление пределов

Если функция является элементарной и если предельное значение аргумента принадлежит ее области определения, то вычисление предела функции сводится к простой подстановке в функцию 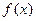предельного значения аргумента, т.е. 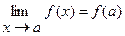. Более сложными являются случаи нахождения пределов функций, где присутствуют неопределенности.

1. «неопределенность типа ».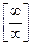

Пример 1. .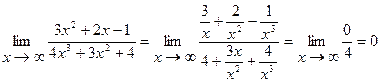

Пример 2. .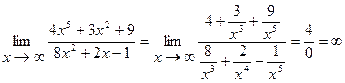

Пример 3. .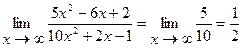

Таким образом, если функция под знаком предела представляет собой отношение многочленов 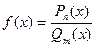, то:

1) 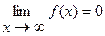, если ;

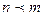2) 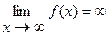, если ;

3) 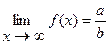, если 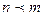. Здесь 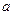и 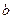- коэффициенты при старших членах многочленов 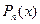и 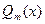соответственно.

Так же вычисляются пределы от иррациональных функций.

2. «неопределенность типа 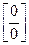». Для вычисления предела 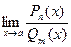необходимо выделить в числителе и знаменателе дроби бином при 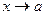, с целью сокращения дроби на множитель, стремящийся к нулю.

Пример 4. .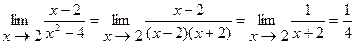

Пример 5. 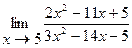. Разлагаем числитель и знаменатель на множители

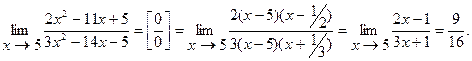
Пример 6. .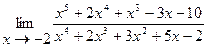

Сократим дробь, разделив числитель и знаменатель на .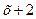

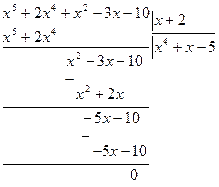и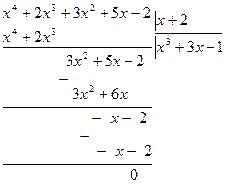

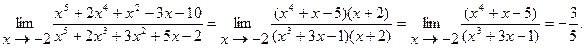
Вообще, если ищется предел дроби, числитель и знаменатель которой многочлены, обращающиеся в нуль в предельной точке 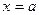, то согласно теореме Безу оба многочлена разделятся без остатка на 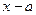, т.е. такую дробь всегда можно сократить на .

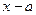Пример 7.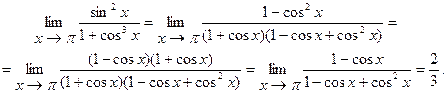

Пример 8.

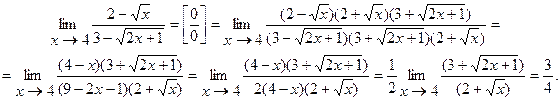
Пример 9. 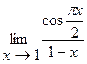. Сделаем замену переменно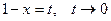й: при . Имеем

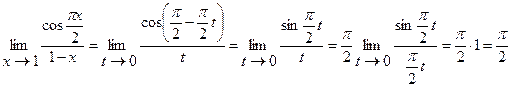
3. «неопределенность типа 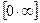». Перейти к 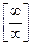или .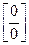

Дата добавления: 2015-07-25