Эквивалентные бесконечно малые

Второй замечательный предел

,

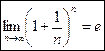Число называется неперовым числом. Оно иррационально, его приближенное (с точностью до сотых) значение равно 2,72.

Справедливы формулы

, , , , ,

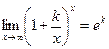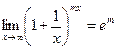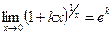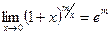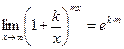Пример 3.

.

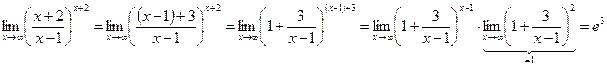Эквивалентные бесконечно малые

Две б.м.в. 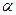и 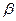называются эквивалентными при 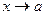, если 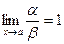. Обозначение 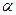~ 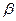. Так, например, 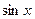~ 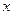, т.к. 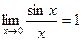, 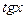~ 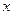, т.к. .

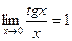Т.1 Предел отношения двух б.м. функций не изменится, если каждую или одну из них заменить эквивалентной б.м., т.е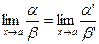

Т.2 Разностьдвух эквивалентных б.м. функций есть бесконечно малая более высокого порядка, чем каждая из них.

Т.3. Сумма конечного числа б.м.ф. разных порядков эквивалентна слагаемому низшего порядка.

Пример 1. ,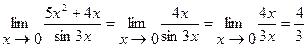

Пример 2. .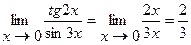

Дата добавления: 2015-07-25