при поперечном изгибе

Нормальные напряжения по высоте сечения изменяются по линейному закону, и для произвольной точки поперечного сечения балки при изгибе определяется по формуле

,

где М_z – изгибающий момент в рассматриваемом поперечном сечении;

у – расстояние рассматриваемой точки сечения до нейтральной оси;

I_z – момент инерции сечения относительно нейтральной оси z.

Касательные напряжения в произвольной точке поперечного сечения балки при изгибе определяется по формуле Журавского:

,

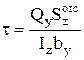где – статический момент отсеченной части, вычисленной относительно

главной центральной оси z;

b_y – ширина сечения по линии обреза m−n, проходящей через точку в которой определяется напряжение.

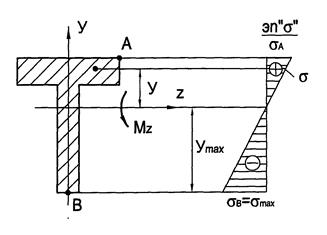
Максимальные нормальные напряжения в сечении балки при изгибе определяется по формуле:

,

где – осевой момент сопротивления сечения относительно оси z,

y_max – расстояние от нейтральной оси z до наиболее удаленных волокон.

Условия прочности при поперечном изгибе имеют вид:

при расчете по допускаемым напряжениям:

;

;

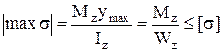при расчете по предельному состоянию:

;

.

Дата добавления: 2015-07-25