Касательные напряжения при кручении

где М− внешний скручивающий момент;

М_к – крутящий момент инерции;

ρ – расстояние от произвольной точки поперечного сечения до

продольной оси вала;

I_р– полярный момент инерции сечения.

Касательное напряжение τ направлено перпендикулярно радиусу ρ.

Максимальные касательные напряжения в точках, наиболее удаленные от оси вала имеют значения:

,

где – полярный момент сопротивления круглого сечения,

r_max – расстояние от оси вала до наиболее удаленных точек

сечения.

Полярный момент инерции и полярный момент сопротивления для вала круглого сечения:

;

.

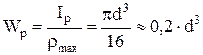, величину этого коэффициента можно задавать в пределах от 0,6 ≤ a ≤ 0,8;

;

.

Угол закручивания φ вала при кручении на участке длиной ℓопределяется по формуле закона Гука в развернутой форме:

, при М_k = соnst, GI_p = соnst,

где GI_p – жесткость поперечного сечения вала при кручении.

Если брус имеет несколько участков, то угол поворота вала определяется как алгебраическая сумма углов закручивания всех его участков

.

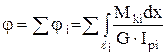Условия прочности и жесткости вала при кручении:

,

,

где [q] – допускаемый угол закручивания вала (рад/м).

В случае если [θ°] − допускаемый угол закручивания задается в град/м, то

.

Приложение 6

Дата добавления: 2015-07-25