
Читайте также:
|
Рассмотрим подключение цепи RC к источнику постоянного напряжения.
Пусть ключ SW находится в положении 1.
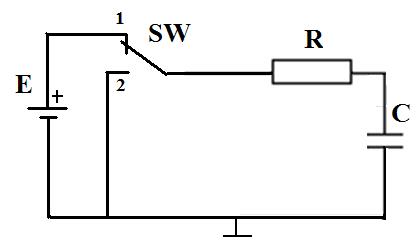
Запишем для этой цепи второй закон Кирхгофа: E = UR + UC;
где UС - падение напряжения на емкости,
UR - падение напряжения на активном сопротивлении.
Учитывая, что ток в цепи i = C*dUc/dt,
а падение напряжения на резисторе UR= i*R =R* C*dUc/dt,
получим Uc + R* C*dUc/dt = E
или dUc/dt + Uc/(R* C)= E/ (R* C).
Полученное равенство представляет собой линейное дифференциальное уравнение первого порядка с неизвестной функцией UC.
В результате решения уравнения можно получить, что UC= E *[1 –exp(- t/t)].
Из выражения видно, что напряжение на емкости в процессе заряда возрастает по экспоненциальному закону, стремясь к величине E. Скорость заряда емкости зависит от постоянной времени цепи: чем больше значения емкости и активного сопротивления, определяющих t, тем медленнее растет напряжение UC.
Ток в цепи описывается соотношением: i = C*dUc/dt = (E/R) * exp(- t/t).
Напряжение на сопротивлении изменяется по закону: UR = E * exp(- t/t).

Из анализа переходных характеристик можно сделать выводы:
1 При t ® 0 сопротивление конденсатора ХС ® 0.
2 При t ® ¥ (t > 5t) сопротивление конденсатора ХС ® ¥.
Дата добавления: 2015-07-25; просмотров: 104 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дифференцирующие цепи. Переходная характеристика. | | | Электронно-дырочный переход и его свойства. |