
Читайте также:
|
Дифференцирующей называется цепь, сигнал на выходе который пропорционален производной от входного воздействия.
Простейшая дифференцирующая цепь имеет вид:
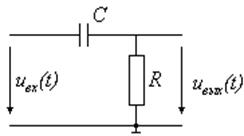
Запишем для этой цепи второй закон Кирхгофа: UC+ UR= Uвх(t);
где UC - падение напряжения на емкости,
UR - падение напряжения на активном сопротивлении.
На участке дифференцирования должно выполняться условие: UC>> UR
Поэтому можно записать, что UC» Uвх(t).
Ток, протекающий в цепи, i» i C» C*(dUC/dt)» C*[d Uвх(t) /dt],
а выходное напряжение описывается соотношением:
Uвых(t)» iC*R» R*C*[d Uвх(t) /dt].
Таким образом, выходное напряжение пропорционально производной от входного воздействия.
Рассмотрим переходные характеристики дифференцирующей цепи.
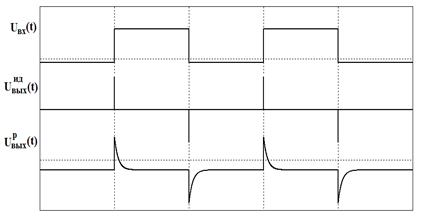
Для обеспечения дифференцирования постоянная времени должна удовлетворять условию t < tW / (50 ¸ 100).
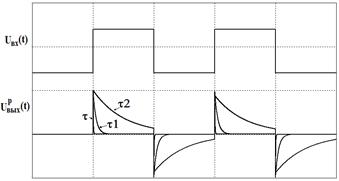
Графики приведены для следующих соотношений:
t = t н= tW / 100; t1 = 10*t н; t2 = 100* t н;
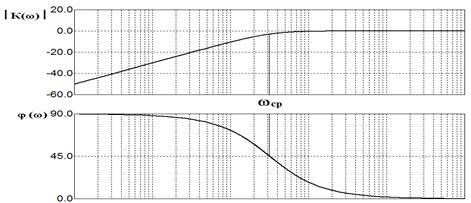
Определим частотные характеристики.
Коэффициент передачи для дифференцирующей цепи.
К(jw) = Uвых(jw) /Uвх(jw).
Выходное напряжение описывается соотношением:
Uвых(jw) = Uвх(jw)*(R / [R + (1/ jw*С)] = Uвх(jw) * jw*R*С / [1 + jw*R*С].
Следовательно
К(jw) = jw*R*С /(1 + jw*R*С) = jw*t / (1 + jw*t).
ЛАЧХ и ЛФЧХ описываются соотношениями:
ôК(w)ôДБ = 20 lg(w*t) - 20 lg [1 + (w*t)2]1/2/.
j (w) = 90°-arctq (w*t).
Применение дифференцирующей цепи:
1 Фильтр высоких частот.
2 Формирователь коротких импульсов.
3 Формирователь отрицательного напряжения.
Дата добавления: 2015-07-25; просмотров: 227 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирующие цепи. Амплитудно-частотная характеристика. | | | Включение в цепь RC постоянного напряжения. |