
Читайте также:
|
Интегрирующей называется цепь, сигнал на выходе который пропорционален интегралу от входного воздействия.
Простейшая интегрирующая цепь имеет вид:
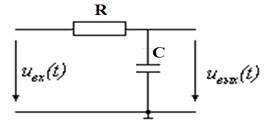
Запишем для этой цепи второй закон Кирхгофа:
UR + UC = Uвх(t);
где UR - падение напряжения на емкости,
UC - падение напряжения на активном сопротивлении.
На участке интегрирования должно выполняться условие: UR>> UС.
Поэтому можно записать, что UR» Uвх(t).
Ток, протекающий в цепи, i» i R» Uвх(t) / R,
а выходное напряжение описывается соотношением:
Uвых(t)» UC» 1/C* ò i*dt» [1/(R*C)]* òUвх(t) *dt].
Таким образом, выходное напряжение пропорционально интегралу от входного воздействия.
Основной параметр интегрирующей цепи – постоянная времени:
t = R*C.
Рассмотрим переходные характеристики интегрирующей цепи.
Переходная характеристика – зависимость от времени выходного напряжения при скачкообразном изменении входного сигнала.
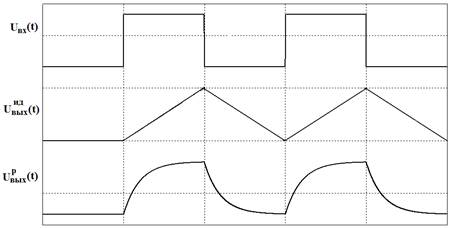
Для обеспечения интегрирования постоянная времени должна удовлетворять условию
t» min{ tW, tП}/ (3 ¸ 5).
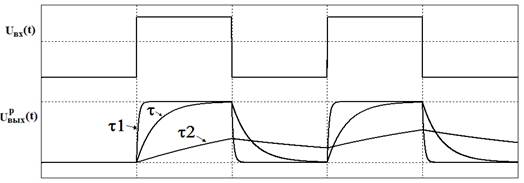
Графики приведены для следующих соотношений:
t = t н =tW / 5; t1 = 0,1*t н; t2 = 10* t н;
Дата добавления: 2015-07-25; просмотров: 160 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Катушки индуктивности. Основные параметры и характеристики. | | | Интегрирующие цепи. Амплитудно-частотная характеристика. |