Выводы из дифференциальных зависимостей

1. Тангенс угла наклона, образованного осью х и касательной к эпюре поперечных сил, в данной точке равен интенсивности распределенной нагрузки:

.

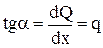2. Тангенс угла наклона, образованного осью Х и касательной к эпюре М, в данной точке равен величине поперечных сил в данной точке:

.

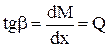3. Если на участке балки:

– поперечная сила больше нуля, то изгибающий момент возрастает слева на право;

– поперечная сила меньше нуля, то изгибающий момент убывает слева на право;

– поперечная сила меняет знак с «+» на «-», то на эпюре изгибающего момента имеем максимум – М_max;

– поперечная сила меняет знак с «-» на «+», то на эпюре изгибающего момента имеем минимум - M_min;

– если поперечная сила равна нулю, то на этом участке имеем чистый изгиб, а величина изгибающего момента постоянна.

4. Если на участке балки интенсивность распределения нагрузки q равна нулю, то эпюра поперечной силы ограничена прямой, параллельной оси, а эпюра изгибающего момента ограничена прямой, наклоненной к оси.

5. Если на участке балки интенсивность распределенной нагрузки q постоянна по величине, то эпюра поперечной силы ограничена прямой, наклоненной к оси х, а эпюра М ограничена квадратной параболой, выгнутой в сторону действия распределенной нагрузки, при построении эпюры изгибающих моментов со стороны растянутых волокон.

6. Под сосредоточенной силой на эпюре Q имеем скачок на величину этой силы, а на эпюре М имеем излом в сторону действия этой силы.

7. Под сосредоточенным внешним моментом на эпюре М имеем скачок на величину этого момента, а на эпюре Q это непосредственно не отражается.

8. В шарнирах изгибающий момент равен нулю, если там не приложены внешние пары сил.

Дата добавления: 2015-07-25