Изучение перпендикулярных прямых

4.1 На плоскости: «Две пересекающиеся прямые называются перпендикулярными (или взаимно-перпендикулярными), если они при пересечении образуют прямые углы»[5]. Так же автор определяет перпендикулярные прямые в пространстве: «Две прямые называются взаимно перпендикулярными (перпендикулярными), если угол между ними равен 90⁰»[6]. Это определение предлагается после введения понятия угла между прямыми (в том числе и скрещивающимися).

4.2 Основные геометрические положения, изучаемые в планиметрии:

1. «Если две прямые плоскости перпендикулярны третьей прямой этой плоскости, то они не пересекаются»[7].

2.Существование и единственность перпендикуляра, проведенного из точки к прямой: «Из точки, не лежащей на прямой в плоскости, можно провести единственный перпендикуляр к данной прямой»[8]. Аналогичное утверждение можно сформулировать для случая, когда точка принадлежит прямой.

3. Задача о построении прямой, перпендикулярной заданной (с помощью циркуля и линейки).

4.3 Основные геометрические положения, изучаемые в стереометрии:

1. Аналогично плоскостному варианту рассматривается задача о построении прямой, перпендикулярной заданной

а) через точку, лежащую на заданной прямой,

б) через точку, не лежащую на заданной прямой.

В пространственном случае особое внимание следует обращать на вопрос о количестве перпендикулярных прямых, их взаимном расположении, о перпендикулярности скрещивающихся прямых.

2. Теорема о трех перпендикулярах.

b_{1 b c}  

Изучение этой теоремы можно начинать с решения двух задач на одном чертеже. a

α

Прямая b принадлежит плоскости α, прямая а пересекает плоскость α, прямая с – проекция прямой а на плоскость α.

1) Прямая b перпендикулярна прямой с. Как в пространстве расположены прямые b и с?

2) Прямая b перпендикулярна прямой а. Как в пространстве расположены прямые b и а?

Отдельно следует рассмотреть случай, когда прямые b и с не пересекаются.

Важно, чтобы ученики не только могли формулировать эти свойства, но и могли их распознавать при решении задач. Поэтому полезно предлагать задачи, в которых комбинация трех прямых расположена нестандартно.

Задача (предлагается после изучения перпендикулярности прямой и плоскости):

Из двух точек на плоскости α. расстояние между которыми а. проведены параллельные наклонные, составляющие углы φ с плоскостью α. Определить расстояние между наклонными, если расстояние между их проекциями на плоскость равно в.

При изучении взаимного расположения прямых в пространстве целесообразно использовать аналогию, предлагая ученикам формулировать самим стереометрические утверждения. Можно использовать аналогию и при различных доказательствах. Например, на плоскости доказано, что две прямые, пересекающие третью, параллельны тогда и только тогда, когда они ей перпендикулярны.

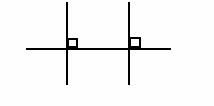
Разумно предложить учащимся рассмотреть эту же геометрическую ситуацию в пространстве и установить условие, при котором выполняется сформулированное для плоскости утверждение.

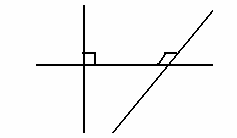
Практически все доказательства разумно предлагать проводить учащимся самостоятельно, используя аналитический путь поиска доказательства (для того, чтобы доказать...., достаточно доказать....).

Дата добавления: 2015-07-25