Задание 3. В соответствии с методом инвариантных импульсных характеристик синтезировать

В соответствии с методом инвариантных импульсных характеристик синтезировать рекурсивные цифровые фильтры первого порядка, используя в качестве аналоговых фильтров прототипов рассмотренные ранее два фильтра ФНЧ (один – фильтр Баттерворта первого порядка, второй – выбирается из Таб.4 в соответствии с номером Вашего варианта). Зарисовать и сравнить АЧХ синтезированных фильтров, исходных аналоговых фильтров и трансверсальных фильтров.

Указания к выполнению Задания 3. Учтем, что системная функция рекурсивного фильтра первого порядка в соответствии с (6) имеет вид

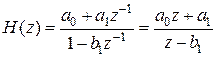. (8)

Для определения коэффициентов 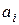и 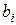поступим следующим образом. Учтем, что системная функция рекурсивного фильтра удовлетворяет соотношению 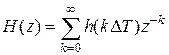, причем 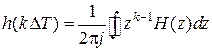. Подставляя в последнее выражение системную функцию (8) и вычисляя интеграл, получаем (получить самостоятельно)

.

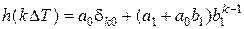Здесь 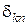− символ Кронекера. Полагая в последнем выражении k = 0,1 и 2 соответственно, получим систему из трех уравнений с тремя неизвестным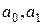и и 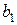. Решая эту систему (решить самостоятельно), получаем

, .

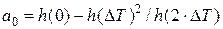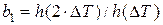
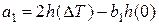Таким образом, системная функция ЦФ найдена. Частотный коэффициент передачи рекурсивного фильтра находим из системной функции аналогично (2), (7). Выводим на экран компьютера на один график АЧХ двух синтезированных рекурсивных фильтров, двух аналоговых фильтров прототипов и двух синтезированных ранее трансверсальных фильтров. Сделать выводы о характере поведения указанных характеристик.

Дата добавления: 2015-07-20