
Читайте также:
|
1.1. Четырехполюсник
Полюсом называют вывод (контакт, клемму, зажим) электрической цепи, к которому что-либо подключается (источник сигнала, нагрузка, другая цепь). Электрические цепи классифицируют по числу полюсов на:
- двухполюсники (сопротивление, индуктивность, емкость, идеальные и реальные источники сигнала, полупроводниковый диод);
- трехполюсники (например, трехфазный источник напряжения без нейтрали, трехфазная нагрузка при соединении «треугольником» на рис. 1.1, биполярный транзистор);
- четырехполюсники (усилители сигналов, фильтры).
Значительно реже возникают цепи с большим числом полюсов.
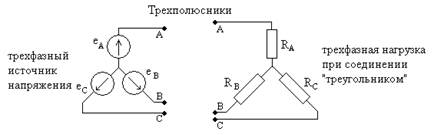
Рис. 1.1
 Четырехполюсником называют электрическую цепь с четырьмя полюсами, разделенными на пару входных и пару выходных полюсов, как показано на рис. 1.2. Входные полюсы обычно изображаются сле-
Четырехполюсником называют электрическую цепь с четырьмя полюсами, разделенными на пару входных и пару выходных полюсов, как показано на рис. 1.2. Входные полюсы обычно изображаются сле-
Рис. 1.2 ва и имеют индекс 1, а вы-
ходные – справа с индексом 2. Входной и выходной токи чаще всего обозначают втекающими в четырехполюсник.
Различают линейные (содержащие только линейные элементы) и нелинейные (в состав которых входит хотя бы один нелинейный элемент) четырехполюсники (рис.1.3).

Рис. 1.3
Свойства линейных четырехполюсников рассматривают при гармонических воздействиях (это простые сигналы, расчет которых удобно проводить методом комплексных амплитуд).
В линейном четырехполюснике при гармоническом воздействии все токи и напряжения являются также гармоническими с той же частотой, а их амплитуды и начальные фазы зависят от частоты воздействия. В этом случае свойства цепи описывают частотными характеристиками – зависимостями от частоты входного сигнала различных характеристик, например:
- входного и выходного сопротивлений или проводимостей;
- коэффициентов передачи или обратной связи по току или напряжению;
- коэффициента передачи мощности;
- сопротивлений (проводимостей) прямой передачи или обратной связи.
1.2 Входное и выходное сопротивления
четырехполюсника
В качестве частотных характеристик рассматриваются входное  и выходное
и выходное  сопротивления как функция частоты сигнала. По определению при заданном сопротивлении нагрузки четырехполюсника
сопротивления как функция частоты сигнала. По определению при заданном сопротивлении нагрузки четырехполюсника  , подключенной к его выходу,
, подключенной к его выходу,
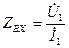 . (1.1)
. (1.1)
Выходное сопротивление определяется при известном внутреннем сопротивлении источника входного сигнала  ,
,
 . (1.2)
. (1.2)
Знание этих характеристик необходимо при анализе возможностей подключения к четырехполюснику реального источника сигнала и нагрузки.
Рассмотрим четырехполюсник с подключенными к нему реальным источником напряжения  с внутренним сопротивлением
с внутренним сопротивлением  и нагрузкой
и нагрузкой  , как показано на рис. 1.4.
, как показано на рис. 1.4.

Рис.1.4
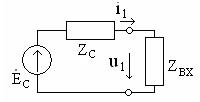 Эквивалентная схема вход-ной цепи четырехполюсника показана на рис. 1.5, где
Эквивалентная схема вход-ной цепи четырехполюсника показана на рис. 1.5, где  - входное сопротивление четырехполюсника. Если необходимо обеспечить максимум амплитуды входного напряже- Рис. 1.5
- входное сопротивление четырехполюсника. Если необходимо обеспечить максимум амплитуды входного напряже- Рис. 1.5
ния  , то по закону Ома полу-
, то по закону Ома полу-
чим
 . (1.3)
. (1.3)
Представляя  и
и  , можно записать
, можно записать
 . (1.4)
. (1.4)
Для идеального источника напряжения  и входное напряжение равно ЭДС источника. Если обеспечить условие максимума
и входное напряжение равно ЭДС источника. Если обеспечить условие максимума  по
по 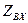 ,
,
 , (1.5)
, (1.5)
то из (1.4) следует
 . (1.6)
. (1.6)
и при условии  входное напряжение
входное напряжение  четырехполюсника станет больше ЭДС источника сигнала.
четырехполюсника станет больше ЭДС источника сигнала.
Это обусловлено резонансными явлениями во входной цепи, которые будут рассматриваться в дальнейшем.
Для обеспечения максимума мощности  , потребляемой четырехполюсником от источника сигнала, из общего выражения
, потребляемой четырехполюсником от источника сигнала, из общего выражения
 , (1.7)
, (1.7)
где  - комплексно сопряженная амплитуда входного тока, получим
- комплексно сопряженная амплитуда входного тока, получим
 , (1.8)
, (1.8)
где  - комплексно-сопряженная ЭДС источника, а
- комплексно-сопряженная ЭДС источника, а  - оператор вычисления реальной части числа. С учетом того, что произведение комплексно-сопряженных чисел равно квадрату их модуля,
- оператор вычисления реальной части числа. С учетом того, что произведение комплексно-сопряженных чисел равно квадрату их модуля,
 , (1.9)
, (1.9)
в результате получим
 . (1.10)
. (1.10)
Из полученного выражения нетрудно получить условие максимума потребляемой четырехполюсником (рис. 3.6) мощности (условие согласования источника сигнала с четырехполюсником),
 (1.11)
(1.11)
Аналогичный анализ можно провести и для выходной цепи четырехполюсника. В соответствии с теоремой об эквивалентном источнике напряжения (повторите этот материал) эквивалентная схема выходной цепи схемы рис. 1.4 имеет вид, показанный на рис. 1.6а, где  и
и  - эквивалентные ЭДС и внутреннее сопротивление активного двухполюсника, показанного на рис. 1.6б, а
- эквивалентные ЭДС и внутреннее сопротивление активного двухполюсника, показанного на рис. 1.6б, а  .
.

Рис. 1.6
Мощность в нагрузке аналогично (1.10) равна
 , (1.12)
, (1.12)
где  и
и  . В результате нетрудно получить условие передачи максимума мощности от источника сигнала через четырехполюсник в нагрузку (условие согласования четырехполюсника с нагрузкой),
. В результате нетрудно получить условие передачи максимума мощности от источника сигнала через четырехполюсник в нагрузку (условие согласования четырехполюсника с нагрузкой),
 (1.13)
(1.13)
В качестве примера рассмотрим цепь на рис. 1.7, в состав которой входят источник входного сигнала (реальный источник гармонического напряжения с комплексной амплитудой  , внутренним сопротивлением
, внутренним сопротивлением  и частотой
и частотой 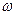 ), RC - четырехполюсник и нагрузка
), RC - четырехполюсник и нагрузка  .
.

Рис. 1.7
Схема цепи для определения входного сопротивления нагруженного четырехполюсника показана на рис. 1.8. Величина  определяется выражением
определяется выражением
 .
.

Рис. 1.8
При активной нагрузке  , умножая числитель и знаменатель дроби на комплексно-сопряженный множитель, получим
, умножая числитель и знаменатель дроби на комплексно-сопряженный множитель, получим
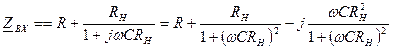 ,
,
модуль входного сопротивления равен
 ,
,
а активную  и реактивную
и реактивную 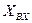 составляющие можно записать в виде
составляющие можно записать в виде
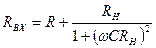 ,
,
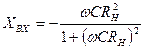 .
.
На рис. 1.9 приведены зависимости от частоты модуля  и активной составляющей
и активной составляющей  входного сопротивления четырехполюсника при
входного сопротивления четырехполюсника при 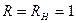 кОм и
кОм и  нФ.
нФ.

Рис. 1.9
На рис. 1.10 показана зависимость от частоты реактивной составляющей входного сопротивления четырехполюсника.
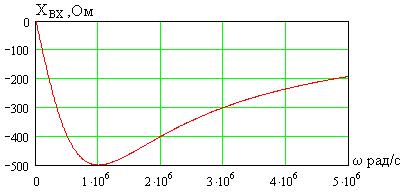
Рис. 1.10
Как видно, входное сопротивление четырехполюсника существенно изменяется в выбранном диапазоне частот и имеет емкостный характер. Модуль и активная составляющая сопротивления уменьшаются с ростом частоты от значения  при
при 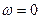 до
до 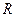 на бесконечной частоте (на высоких частотах емкость шунтирует нагрузку).
на бесконечной частоте (на высоких частотах емкость шунтирует нагрузку).
Рассмотрим, каким должно быть внутреннее сопротивление источника сигнала, чтобы обеспечить передачу максимума мощность в четырехполюсник на частоте 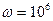 рад/с.
рад/с.
В этом случае входное сопротивление четырехполюсника равно  Ом. Тогда в соответствии с (1.11) источник сигнала должен иметь внутреннее сопротивление равным
Ом. Тогда в соответствии с (1.11) источник сигнала должен иметь внутреннее сопротивление равным  Ом. Характер трехмерной зависимости мощности
Ом. Характер трехмерной зависимости мощности  от активной
от активной  и реактивной
и реактивной 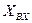 составляющих входного сопротивления четырехполюсника в соответствии с (1.10) при
составляющих входного сопротивления четырехполюсника в соответствии с (1.10) при  В показан на рис. 1.11. Максимум
В показан на рис. 1.11. Максимум  имеет место при условии (1.11).
имеет место при условии (1.11).
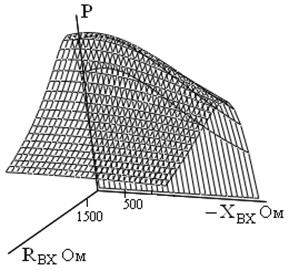
Рис. 1.11
Подставляя в (1.10) выражения для активной  и реактивной
и реактивной 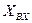 составляющих для цепи рис. 1.7, получим зависимость потребляемой четырехполюсником мощности
составляющих для цепи рис. 1.7, получим зависимость потребляемой четырехполюсником мощности  от частоты сигнала. Она показана на рис. 1.12 при
от частоты сигнала. Она показана на рис. 1.12 при  В и
В и  Ом.
Ом.
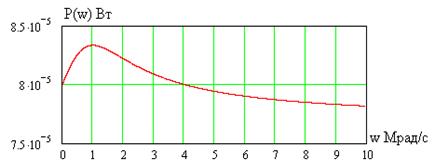
Рис. 1.12
Как видно, на частоте 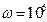 рад/с, когда
рад/с, когда  Ом и выполняется условие согласования (1.11), имеет место максимум потребляемой четырехполюсником мощности.
Ом и выполняется условие согласования (1.11), имеет место максимум потребляемой четырехполюсником мощности.
Рассмотрим выходное сопротивление четырехполюсника рис. 1.7, для этого рассмотрим цепь на рис. 1.13а. В соответствии с теоремой об эквивалентном источнике ее можно заменить эквивалентным реальным источником напряжения, показанным на рис. 1.13б. Эквивалентная ЭДС  равна напряжению холостого хода цепи рис. 1.13а,
равна напряжению холостого хода цепи рис. 1.13а,  , а эквивалентное сопротивление
, а эквивалентное сопротивление  равно сопротивлению цепи рис. 1.13а при выключенном источнике, как показано на рис. 1.14. Сопротивление
равно сопротивлению цепи рис. 1.13а при выключенном источнике, как показано на рис. 1.14. Сопротивление  и есть внутреннее сопротивление четырехполюсника.
и есть внутреннее сопротивление четырехполюсника.

Рис. 1.13
Для цепей на рис. 1.13а и рис. 1.14 нетрудно получить параметры эквивалентного источника рис. 1.13б. Его ЭДС и внутреннее сопротивление  равны
равны
 ,
,
 .
.
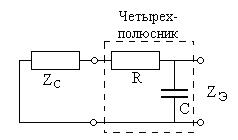
Рис. 1.14
На рис. 1.15 показана программа MathCAD для расчета значений выходного сопротивления  , на рис. 1.16 приведены зависимости от частоты модуля и аргумента
, на рис. 1.16 приведены зависимости от частоты модуля и аргумента  , а на рис. 1.17 – его активной
, а на рис. 1.17 – его активной  и реактивной
и реактивной  составляющих при
составляющих при  кОм,
кОм, 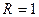 кОм и
кОм и 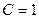 нФ.
нФ.

Рис. 1.15

Рис. 1.16

Рис. 1.17
Как видно, модуль выходного сопротивления максимален на постоянном токе и быстро падает с ростом частоты. Выходное сопротивление всегда имеет емкостный характер. На частоте  рад/с
рад/с  Ом и
Ом и 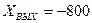 Ом.
Ом.
Для обеспечения максимальной мощности в нагрузке ее сопротивление должно удовлетворять условию (1.13). Проведите самостоятельно анализ, аналогичный показанному на рис. 1.11.

1.3. Комплексный коэффициент передачи
Комплексный коэффициент передачи по напряжению определяется выражением
 , (1.14)
, (1.14)
аналогично вводятся в рассмотрение комплексный коэффициент передачи тока
 (1.15)
(1.15)
и коэффициент (не комплексный) передачи мощности
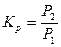 , (1.16)
, (1.16)
где  - мощность, потребляемая четырехполюсником, а
- мощность, потребляемая четырехполюсником, а  - мощность, передаваемая в нагрузку. Для расчета коэффициентов передачи необходимо при заданном источнике входного сигнала определить комплексные амплитуды входного и выходного напряжений, токов или мощностей.
- мощность, передаваемая в нагрузку. Для расчета коэффициентов передачи необходимо при заданном источнике входного сигнала определить комплексные амплитуды входного и выходного напряжений, токов или мощностей.
 В качестве примера рассмотрим четырехполюсник, схема которого показана на рис. 1.12, и определим его комплексный коэффициент передачи напряжения вида (1.14).
В качестве примера рассмотрим четырехполюсник, схема которого показана на рис. 1.12, и определим его комплексный коэффициент передачи напряжения вида (1.14).
Подключим на вход четырехполюс- Рис. 1.18
полюсника идеальный
источник напряжения с ЭДС 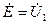 , как показано на рис. 1.13, и воспользуемся методом узловых напряжений. В цепи имеется два узла и необходимо определить единственное узловое напряжение
, как показано на рис. 1.13, и воспользуемся методом узловых напряжений. В цепи имеется два узла и необходимо определить единственное узловое напряжение 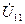 . Выражая через
. Выражая через 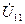 токи ветвей и используя первый закон Кирхгофа, получим уравнение метода узловых напряжений:
токи ветвей и используя первый закон Кирхгофа, получим уравнение метода узловых напряжений:


Рис. 1.19
После алгебраических преобразований получим
 .
.
Тогда по Закону Ома можно определить выходное напряжение
 .
.
Подставляя выражение для 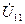 , с учетом
, с учетом  получим
получим
 .
.
Тогда комплексный коэффициент передачи четырехполюсника по напряжению равен
 .
.
Как видно, 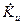 - комплексная функция частоты сигнала,
- комплексная функция частоты сигнала,
ее называют комплексной частотной характеристикой (КЧХ). Графически она отображается линией в трехмерном пространстве (ось 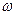 и две оси для отображения комплексного числа), что неудобно практически.
и две оси для отображения комплексного числа), что неудобно практически.
На плоскости КЧХ изображается в виде годографа. Для его построения заданный интервал частот разбивается с равномерным шагом, для каждого значения частоты вычисляются и отображаются на комплексной плоскости по осям абсцисс и ординат соответственно действительная  и мнимая
и мнимая  составляющие комплексного коэффициента передачи.
составляющие комплексного коэффициента передачи.
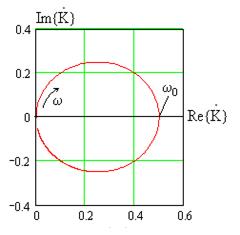 Пример годографа КЧХ цепи на рис. 1.18 при
Пример годографа КЧХ цепи на рис. 1.18 при  кОм,
кОм,  мГн и
мГн и  нФ показан на рис. 1.20. Стрелка показывает направление увеличения частоты входного сигнала. На частоте
нФ показан на рис. 1.20. Стрелка показывает направление увеличения частоты входного сигнала. На частоте

величина  действительна, а точка годографа расположена на оси абсцисс.
действительна, а точка годографа расположена на оси абсцисс.
Рис. 1.20
1.4. Амплитудно-частотная и фазочастотная
характеристики четырехполюсника
Комплексный коэффициент передачи четырехполюсника можно представить в показательной форме,
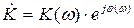 , (1.17)
, (1.17)
где  - его модуль, а
- его модуль, а  - аргумент.
- аргумент.
Амплитудно-частотная характеристика (АЧХ) 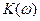 представляет собой зависимость модуля комплексного коэффициента передачи от частоты. Она представляет собой отношение амплитуд или действующих значений выходного сигнала к входному.
представляет собой зависимость модуля комплексного коэффициента передачи от частоты. Она представляет собой отношение амплитуд или действующих значений выходного сигнала к входному.
Дата добавления: 2015-07-25; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ | | | Фазочастотная характеристика (ФЧХ) – это зависимость от частоты аргумента комплексного коэффициента передачи. Она представляет собой сдвиг фаз между выходным и входным сигналами. |