
|
Читайте также: |
КОНТУР
5.1. Схема параллельного колебательного контура
Параллельный колебательный контур представляет собой параллельное соединение катушки индуктивности  и конденсатора
и конденсатора 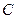 , принципиальная схема которого показана на рис. 5.1а.
, принципиальная схема которого показана на рис. 5.1а.
На рис. 5.1б показана эквивалентная схема параллельного колебательного контура, в которую включено сопротивление потерь  катушки индуктивности, сопротивление потерь конденсатора в большинстве случаев можно не учитывать.
катушки индуктивности, сопротивление потерь конденсатора в большинстве случаев можно не учитывать.
В ряде случаев применяется параллельная эквивалентная схема, показанная на рис. 5.1в, в этом случае сопротивление 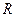 не является сопротивлением потерь контура, хотя и зависит от него. Параллельная модель рис. 5.1в удобна при расчете проводимости цепи.
не является сопротивлением потерь контура, хотя и зависит от него. Параллельная модель рис. 5.1в удобна при расчете проводимости цепи.
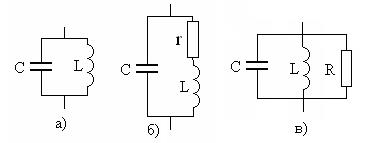
Рис. 5.1
5.2. Входное сопротивление и проводимость
В дальнейшем в основном будем использовать модель параллельного колебательного контура вида рис. 5.1б. Ее комплексное сопротивление определяется выражением
 . (5.1)
. (5.1)
В окрестности частоты 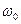 , равной
, равной
 , (5.2)
, (5.2)
пренебрегая в числителе (5.1) величиной  , получим
, получим
 . (5.3)
. (5.3)
Как видно, целесообразно перейти к координатам обобщенной расстройки, рассмотренным в подразделе 3.6,
 , (5.4)
, (5.4)
 - добротность параллельного колебательного контура, равная
- добротность параллельного колебательного контура, равная
 , (5.5)
, (5.5)
 - характеристическое сопротивление контура,
- характеристическое сопротивление контура,
 . (5.6)
. (5.6)
 |
В результате из (5.3) получим выражение для комплексного сопротивления контура в координатах обобщенной расстройки
 , (5.7)
, (5.7)
из которого нетрудно найти модуль  , аргумент
, аргумент  , активную
, активную 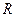 и реактивную
и реактивную  составляющие,
составляющие,

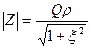 , (5.8)
, (5.8)
 , (5.9)
, (5.9)
 , (5.10)
, (5.10)
 , (5.11)
, (5.11)
(получите эти выражения самостоятельно). Графики этих функций  показаны на рис. 5.2.
показаны на рис. 5.2.


Рис.5.2
На частоте 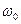 (5.2) сопротивление контура максимально, чисто активно и равно
(5.2) сопротивление контура максимально, чисто активно и равно
 , (5.12)
, (5.12)
графики на рис. 5.2 построены при  кОм (сравните с сопротивлением последовательного контура, которое минимально на этой частоте). При отклонении от частоты
кОм (сравните с сопротивлением последовательного контура, которое минимально на этой частоте). При отклонении от частоты  сопротивление резко падает, появляется реактивная компонента. При
сопротивление резко падает, появляется реактивная компонента. При  сопротивление контура имеет индуктивный характер, а при
сопротивление контура имеет индуктивный характер, а при  - емкостный, этот же результат вытекает и из анализа фазовой характеристики на рис. 5.2б.
- емкостный, этот же результат вытекает и из анализа фазовой характеристики на рис. 5.2б.
Анализ проводимости контура, в том числе и для модели рис. 5.1в, проведите самостоятельно.
5.3. Напряжение и токи в контуре
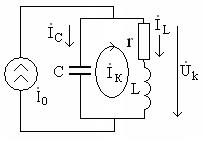
Подключим к параллельному колебательному контуру идеальный источник тока с комплексной амплитудой  , как показано на рис. 5.3, и определим напряжение на параллельных ветвях контура
, как показано на рис. 5.3, и определим напряжение на параллельных ветвях контура 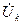 ,
,
 . (5.13)
. (5.13)
Токи  и
и  в реактивных ветвях контура в окрестности частоты
в реактивных ветвях контура в окрестности частоты 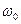 , то есть при условии
, то есть при условии  , соответст-
, соответст-
Рис. 5.3 венно равны
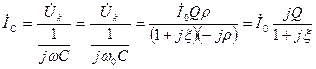 , (5.14)
, (5.14)
 . (5.15)
. (5.15)
Амплитуда и начальная фаза напряжения на контуре определяются выражениями
 , (5.16)
, (5.16)
 , (5.17)
, (5.17)
где  - начальная фаза тока источника. Зависимости амплитуды напряжения
- начальная фаза тока источника. Зависимости амплитуды напряжения  и сдвига фаз
и сдвига фаз  между этим напряжением и током источника
между этим напряжением и током источника  от обобщенной расстройки показаны на рис. 5.4 при
от обобщенной расстройки показаны на рис. 5.4 при  кОм и
кОм и  мА.
мА.
Как видно, кривая  имеет экстремальный характер,
имеет экстремальный характер,
однако резонанс напряжения в параллельном колебательном контуре отсутствует, так как напряжение на контуре всегда равно напряжению на источнике тока.

Рис.5.4
Токи  и
и  в реактивных ветвях контура определяются формулами (5.14) и (5.15), из которых следует
в реактивных ветвях контура определяются формулами (5.14) и (5.15), из которых следует
 или
или  . (5.18)
. (5.18)
Эти равенства нарушают первый закон Кирхгофа
 , (5.19)
, (5.19)
то есть выражения (5.14) и (5.15) являются приближенными (как и все вычисления в координатах обобщенной расстройки).
Амплитуды этих токов одинаковы и равны
 , (5.20)
, (5.20)
а начальные фазы  и
и  определяются соотношениями
определяются соотношениями
 , (5.21)
, (5.21)
 , (5.22)
, (5.22)
Как видно, токи в реактивных ветвях контура противофазны. Зависимости амплитуд токов в реактивных ветвях контура и сдвигов фаз  и
и  между токами в реактивных ветвях и током источника от обобщенной расстройки показаны на рис. 5.5 при
между токами в реактивных ветвях и током источника от обобщенной расстройки показаны на рис. 5.5 при  мГн,
мГн, 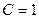 нФ,
нФ,  Ом и
Ом и  мА.
мА.

Рис.5.5
Как видно, токи  и
и  резко возрастают в окрестности точки
резко возрастают в окрестности точки  (или частоты
(или частоты 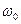 ) по сравнению с амплитудой тока источника, то есть в параллельном колебательном контуре имеет место резонанс токов в реактивных ветвях.
) по сравнению с амплитудой тока источника, то есть в параллельном колебательном контуре имеет место резонанс токов в реактивных ветвях.
Частота 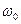 (5.2) является резонансной частотой контура, на которой
(5.2) является резонансной частотой контура, на которой
 , (5.23)
, (5.23)
то есть резонансный ток в реактивных ветвях контура в  раз больше тока источника.
раз больше тока источника.
 Так как токи
Так как токи  и
и  противофазны, то вводят в рассмотрение кольцевой замкнутый ток в контуре
противофазны, то вводят в рассмотрение кольцевой замкнутый ток в контуре  , как показано на рис. 5.6. Он совпадает по направлению с током
, как показано на рис. 5.6. Он совпадает по направлению с током  и поэтому равен
и поэтому равен
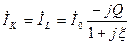 . (5.24)
. (5.24)
Рис. 5.6
Амплитуда контурного тока
равна (5.20), а начальная фаза (5.22), соответствующие графики показаны на рис. 5.5. Резонансный контурный ток в  раз больше тока источника.
раз больше тока источника.
 . (5.25)
. (5.25)
5.4. Вторичные параметры колебательного контура
Параллельный колебательный контур (как и последовательный) полностью описывается своими первичными параметрами  ,
,  и
и 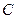 . На практике широко используются вторичные параметры:
. На практике широко используются вторичные параметры:
- резонансная частота контура
 (5.26)
(5.26)
или
 ; (5.27)
; (5.27)
- х арактеристическое сопротивление контура
 ; (5.28)
; (5.28)
- д обротность контура
 . (5.29)
. (5.29)
5.5. Частотные характеристики
Частотные характеристики параллельного колебательного контура представляют собой зависимость от частоты характеристик комплексного коэффициента передачи по току
 (5.30)
(5.30)
или
 , (5.31)
, (5.31)
где  и
и  - комплексные амплитуды токов реактивных ветвей контура,
- комплексные амплитуды токов реактивных ветвей контура,  - комплексная амплитуда тока источника.
- комплексная амплитуда тока источника.
Рассмотрим комплексный коэффициент передачи тока емкости  (аналогичный анализ
(аналогичный анализ 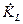 проведите самостоятельно). Из (5.30) с учетом (5.14) получим
проведите самостоятельно). Из (5.30) с учетом (5.14) получим
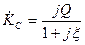 . (5.32)
. (5.32)
Для АЧХ  и ФЧХ
и ФЧХ  контура получим
контура получим
 , (5.33)
, (5.33)
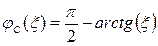 , (5.34)
, (5.34)
где обобщенная расстройка определяется выражением (3.38)
 . (5.35)
. (5.35)
Частотные характеристики параллельного колебательного контура в координатах  вида (5.33) и (5.34) численно совпадают с аналогичными характеристиками для последовательного контура (3.42) и (3.43). Эти зависимости показаны на рис. 5.7 при
вида (5.33) и (5.34) численно совпадают с аналогичными характеристиками для последовательного контура (3.42) и (3.43). Эти зависимости показаны на рис. 5.7 при  .
.

Рис. 5.7
Те же графики в координатах абсолютной расстройки  оказаны на рис. 5.8 при
оказаны на рис. 5.8 при  и
и  рад/с.
рад/с.

Рис. 5.8.
Максимум АЧХ равен  и достигается при
и достигается при  , то есть на резонансной частоте
, то есть на резонансной частоте  . При отклонении частоты от
. При отклонении частоты от 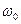 коэффициент передачи резко падает, то есть параллельный колебательный контур может использоваться как узкополосный частотный фильтр.
коэффициент передачи резко падает, то есть параллельный колебательный контур может использоваться как узкополосный частотный фильтр.
Влияние параметров контура на форму частотных характеристик было рассмотрено при анализе последовательного колебательного контура (повторите его самостоятельно)
5.6. Полоса пропускания и коэффициент
прямоугольности
Так как выражение для АЧХ (5.33) параллельного колебательного контура совпадает с аналогичным выражением для последовательного контура, то формулы для полосы пропускания 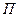 и коэффициента прямоугольности
и коэффициента прямоугольности 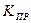 этих контуров совпадают (получите эти результаты еще раз самостоятельно),
этих контуров совпадают (получите эти результаты еще раз самостоятельно),
 , (5.36)
, (5.36)
 . (5.37)
. (5.37)
5.7. Влияние сопротивления источника сигнала и
нагрузки на резонансные свойства контура
Рассмотрим параллельный колебательный контур на рис. 5.9а с реальным источником тока  (
(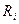 - внутреннее сопротивление источника) и параллельно подключенной нагрузкой
- внутреннее сопротивление источника) и параллельно подключенной нагрузкой 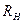 .
.

Рис. 5.9
Параллельное соединение 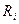 и
и 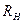 заменяется эквивалентным сопротивлением
заменяется эквивалентным сопротивлением  , как показано на рис. 5.9б, а в этой схеме необходимо преобразовать параллельное соединение
, как показано на рис. 5.9б, а в этой схеме необходимо преобразовать параллельное соединение  и ветви
и ветви  в эквивалентное последовательное соединение
в эквивалентное последовательное соединение 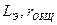 в окрестности резонансной частоты контура
в окрестности резонансной частоты контура 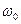 . Найдем сопротивление
. Найдем сопротивление  параллельного соединения,
параллельного соединения,
 , (5.38)
, (5.38)
выделим его действительную и мнимую составляющие и приравняем их составляющим эквивалентного последовательного соединения элементов 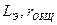 (рис. 5.9в) вида
(рис. 5.9в) вида
 . (5.39)
. (5.39)
В результате получим
 , (5.40)
, (5.40)
 . (5.41)
. (5.41)
Допустим, что сопротивление  много больше величин
много больше величин  и
и  , тогда в окрестности резонансной частоты
, тогда в окрестности резонансной частоты  можно записать
можно записать
 , (5.42)
, (5.42)
 (5.43)
(5.43)
(повторите эти преобразования самостоятельно).
Как видно из (5.42), подключение внутреннего сопротивления источника сигнала и нагрузки приводит к повышению эквивалентных потерь в контуре, эквивалентная добротность которого при этом равна
 . (5.44)
. (5.44)
Полученное выражение совпадает с аналогичной формулой, учитывающей влияние нагрузки в последовательном колебательном контуре (проверьте это самостоятельно).
Подключение реального источника сигнала и нагрузки снижает эквивалентную добротность контура. Чтобы добротность упала незначительно, необходимо выполнение условий
 (5.45)
(5.45)
Например, если  , то
, то  , то есть добротность значительно снижается, а если
, то есть добротность значительно снижается, а если  , то
, то  .
.
Реализовать условие (5.45) достаточно сложно, а часто и невозможно и требуются использование неполного включения контура к источнику сигнала и нагрузке, как показано на рис. 5.10. Можно показать, что эквивалентная добротность в этом случае равна
 , (5.46)
, (5.46)
где
 и
и 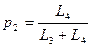 (5.47)
(5.47)

- коэффициенты включения в контур источника сигнала и нагрузки. Их значения выбираются достаточно малыми (например, 0,1), что существенно ослабляет влияние на добротности сопротивлений 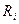 и
и 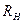 ,.которые должны Рис. 5.10
,.которые должны Рис. 5.10
удовлетворять условиям
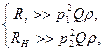 (5.48)
(5.48)
что значительно проще реализовать, чем (5.45).
Колебательные контуры вида рис. 5.10 называют сложными параллельными колебательными контурами. Помимо резонанса токов на частоте 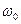 , равной
, равной
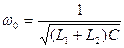 , (5.49)
, (5.49)
имеется резонанс напряжений в последовательном колебательном контуре  на частоте
на частоте
 . (5.50)
. (5.50)
Рабочим является интервал частот в окрестности 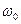 , в котором сопротивление контура в точках подключения источника сигнала в координатах обобщенной расстройки равно
, в котором сопротивление контура в точках подключения источника сигнала в координатах обобщенной расстройки равно
 . (5.51)
. (5.51)
5.8. Расчеты цепей с параллельными колебательными
контурами
Если в составе цепи имеется параллельный колебательный контур, то ее расчет целесообразно проводить в координатах обобщенной расстройки. Рассмотрим цепь, показанную на рис. 5.11 при  Ом,
Ом, 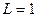 мГн,
мГн, 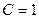 нФ,
нФ,  кОм, в нее
кОм, в нее
 включен источник гармонических колебаний с комплексной амплитудой
включен источник гармонических колебаний с комплексной амплитудой  В и частотой
В и частотой  рад/с.
рад/с.
В состав цепи входит параллельный колебатель- Рис. 5.11
ный контур  , его
, его
резонансная частота 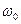 , добротность
, добротность  и обобщенная расстройка
и обобщенная расстройка  соответственно равны
соответственно равны
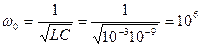 рад/с,
рад/с,
 ,
,
 .
.
Вычислим комплексное сопротивление контура  в координатах обобщенной расстройки,
в координатах обобщенной расстройки,
 кОм.
кОм.
Тогда ток  равен
равен
 мА,
мА,
а напряжение на емкости -
 В.
В.
 Рассмотрим цепь со сложным параллельным колебательным контуром, показанную на рис. 5.12. приняв
Рассмотрим цепь со сложным параллельным колебательным контуром, показанную на рис. 5.12. приняв  мГн,
мГн,  мГн и оставив остальные исходные данные теми же, что и для цепи на рис. 5.11. Коэффициент включения источника в контур равен
мГн и оставив остальные исходные данные теми же, что и для цепи на рис. 5.11. Коэффициент включения источника в контур равен
 ,
,
Рис. 5.12
а общая индуктивность контура соответственно  мГн, при этом резонансная частота, добротность и обобщенная расстройка будут такими же, как и в предыдущей задаче.
мГн, при этом резонансная частота, добротность и обобщенная расстройка будут такими же, как и в предыдущей задаче.
Сопротивление контура в точках подключения источника определяется выражением
 Ом,
Ом,
ток равен
 мА,
мА,
а напряжение на емкости соответственно
 В.
В.
5.9. Моделирование параллельного колебательного
контура
Проведем схемотехническое моделирование цепи, показанной на рис. 5.11 в пакете MicroCAP7, схема модели представлена на рис. 5.13, частота источника  157,6 кГц (
157,6 кГц ( рад/с).
рад/с).

Рис. 5.13
В верхней части рис. 5.14 показаны полученные в результате моделирования временные реализации напряжений в узлах 1 (пунктир) и 2, которые на рис 5.13 отмечены цифрами в кружках. В его нижней части показаны временные диаграммы токов в неразветвленной части контура - тока источника (кривая с маленькой амплитудой) и токов в емкостной (пунктир) и индуктивной ветвях контура. На начальном интервале времени 60 мкс (60u) наблюдается переходной процесс, а затем колебания устанавливаются и можно проводить измерения (убедитесь самостоятельно, что результаты расчета и моделирования совпадают).
Как видно, токи в индуктивности и емкости противофазны, их амплитуды одинаковы и много больше амплитуды тока источника, то есть в параллельном колебательном контуре имеет место резонанс токов.
На рис. 5.15 приведены частотные характеристики цепи по передаче напряжения от узла 1 к узлу 2, по которым нетрудно определить напряжение на емкости (в узле 2).




5.10. Применение параллельного колебательного
контура
Параллельный колебательный контур чаще всего используется как элемент частотного фильтра аналогично последовательному контуру (пример будет рассмотрен далее), или как нагрузка активного элемента (транзистора) в резонансном усилителе сигнала. Пример схемы такого усилителя в моделирующем пакете MicroCAP7 показан на рис. 5.16.

Рис. 5.16
В состав усилителя входит импортный биполярный транзистор  типа 2N5190 (можно использовать отечественный аналог) с цепями питания по постоянному току
типа 2N5190 (можно использовать отечественный аналог) с цепями питания по постоянному току  от источника
от источника  постоянного напряжения 15В, параллельный колебательный контур
постоянного напряжения 15В, параллельный колебательный контур 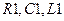 и источник гармонического входного сигнала с частотой
и источник гармонического входного сигнала с частотой  159,15 кГц.(
159,15 кГц.( рад/с), совпадающей с резонансной частотой контура, и амплитудой 4 мВ.
рад/с), совпадающей с резонансной частотой контура, и амплитудой 4 мВ.
На рис. 5.17 показаны временные диаграммы напряжений источника (верхняя кривая), выходного напряжения на коллекторе транзистора в узле 4 (нижняя кривая) и там же постоянное напряжение питания.

На рис. 5.18 представлены частотные характеристики резонансного усилителя (верхняя кривая – АЧХ, нижняя – ФЧХ). Коэффициент усиления равен примерно 3000 на частоте 151,6 кГц, что следует и из кривых на рис 5.17: амплитуда входного сигнала равна 3 мВ, а выходного 8,36 В (максимум АЧХ на рис. 5.18 несколько выше измеренного по временным диаграммам, так как она моделируется при весьма слабом сигнале).

Рис. 5.18
Проведите моделирование рассмотренной цепи самостоятельно, изменяя ее параметры. Введите неполное включение транзистора к контуру, сравните результаты.
5.11. Задания для самостоятельного решения
Задание 5.1. Вычислите резонансное сопротивление параллельного колебательного контура при 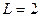 мГн,
мГн,  пФ,
пФ,  Ом.
Ом.
Задание 5.2. Определите резонансную частоту контура
при  кОм и С=1 нФ.
кОм и С=1 нФ.
Задание 5.3. Найдите напряжение на емкости параллельного контура в цепи рис. 5.19 при 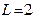 мГн,
мГн,  пФ,
пФ,  Ом,
Ом,  В,
В,  кОм,
кОм,  рад/с. Расчет проведите в координатах обобщенной расстройки.
рад/с. Расчет проведите в координатах обобщенной расстройки.
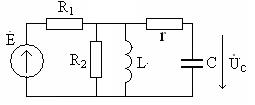
Рис. 5.19
Задание 5.5. Получите выражение для АЧХ цепи, показанной на рис. 5.20. Постройте график АЧХ при  мГн,
мГн,  пФ,
пФ,  Ом,
Ом,  кОм. Проведите расчет в координатах обобщенной расстройки и абсолютной частоты, сравните результаты.
кОм. Проведите расчет в координатах обобщенной расстройки и абсолютной частоты, сравните результаты.

Рис. 5.20
Дата добавления: 2015-07-25; просмотров: 149 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПОСЛЕДОВАТЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ | | | СЛОЖНЫЕ ЧАСТОТНЫЕ ФИЛЬТРЫ |