Параллельный перенос осей координат

Общее уравнение второго порядка относительно и приведено ранее. Однако, уравнение целесообразно записывать в следующем виде:

,

()

как в большинстве формул преобразований входят коэффициенты при , , деленные на два.

Пусть в уравнении () коэффициент , тогда оно имеет вид

,

()

Задача состоит в том, чтобы при помощи преобразования координат привести уравнение () к каноническому виду, т.е., зная уравнение некоторой линии в одной системе координат (назовем ее старой), найти уравнение линии той же линии в другой системе координат (назовем ее новой). Новую прямоугольную систему координат будем получать из старой системы прямоугольных координат с помощью параллельного переноса начала координат.

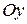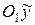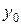Пусть заданы две системы декартовых прямоугольных координат с разными началами и и одинаковыми направлениями осей. Будем называть , старыми, а , новыми координатными осями. Обозначим через и – координаты нового начала в старой системе. Спроецируем произвольную точку 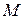на ос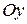и , и , , 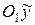тогда из рисунка видно, что (см. рис. )

	Рис. .

Таким образом, получены формулы, позволяющие выразить старые координаты и через новые и . Итак, формулы параллельного переноса осей имеют вид:

или
		()

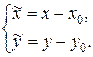
Новые оси и 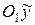параллельны старым. Точка является центром эллипса или гиперболы и вершиной в случае параболы.

Приведение уравнения () к каноническому виду удобно выполнять методом выделения полных квадратов.

Пример 3.5.1. Найдите координаты фокусов эллипса

.

Решение. Полуоси данного эллипса , . Таким образом, фокусное расстояние . Центр эллипса находится в точке . Следовательно, фокусы находятся в точках , .

Ответ: , .

Пример 3.5.2. Уравнение линии второго порядка привести к каноническому виду. Найти координаты фокусов. Сделать чертеж.

Решение. Группируем члены, содержащие только 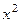и 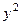за скобку:

.

Дополняем выражения в скобках до полных квадратов:

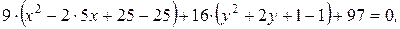
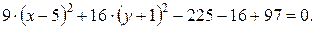
Таким образом, данное уравнение преобразовано к виду

.

Обозначаем или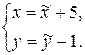

Сравнивая с уравнениями (), видим, что эти формулы определяют параллельный перенос осей координат в точку . В новой системе координат уравнение запишется так:

.

Перенеся свободный член уравнения вправо и разделив на него, получим

Итак, данная линия второго порядка есть эллипс с полуосями , 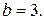Центр эллипса находится в новом начале координат , а его фокальная ось есть ось Расстояние фокусов от центра = , так что новые координаты правого фокуса : , . Старые координаты этого же фокуса находятся из формул параллельного переноса:

, .

Аналогично, новые координаты левого фокуса : , . Его старые координаты: ,

Чтобы начертить данный эллипс, наносим на чертеж старые и новые координаты оси. По обе стороны от точки откладываем по оси отрезки длины , а по оси – длины получив, таким образом, вершины эллипса, сделаем чертеж (рис. ).

0 1     Рис. .

Замечание. Для уточнения чертежа полезно найти точки пересечения данной линии со старыми координатами осями. Для этого надо в формуле () положить сначала , а затем и решить полученные уравнения. Появление комплексных корней будет означать, что линия соответствующую координатную ось не пересекает.

Например. Для эллипса, рассмотренного в примере , получим уравнения:

, .

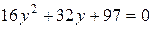Второе из этих уравнений имеет комплексные корни, так что эллипс ось не пересекает. Корни первого уравнения:

, .

В точках и 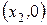эллипс пересекает ось 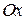(см. рис. ).

Пример 3.5.3. Преобразовать к каноническому виду уравнение линии

.

Найти координаты фокусов. Сделать чертеж.

Решение. Выделим полные квадраты по переменным и :

.

Откуда

.

Разделим обе части уравнения на 9:

.

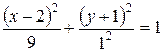Введем новую систему координат с началом в точке , получающуюся из старой параллельным переносом. получим, что кривая задается уравнением

.

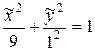Получено каноническое уравнение эллипса с полуосями и .

Из формулы (3.2.4) . Поэтому фокусы в новой системе координат имеют координаты , . Используя формулы (), находим старые координаты фокусов , 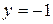. Таким образом, фокусами являются точки и . Сделаем чертеж (рис. ).

Рис. .

Пример3.5.4. Уравнение линии второго порядка

привести к каноническому виду. Определить вид и расположение линии, найти координаты фокусов. Сделать чертеж.

Решение. Выделяем сначала полные квадраты по и по :

,

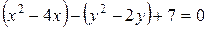Далее, обозначаем или

Геометрически это означает, что мы делаем параллельный перенос осей координат в точку [сравнить с формулой ()]. После параллельного переноса получим

или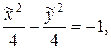

т.е. уравнение гиперболы, центр которой расположен в точке Так как ее полуоси равны , то это равносторонняя гипербола, действительная ось который направлена по оси 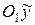. На этой оси расположены фокусы и на расстоянии 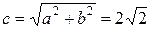от центра .

Следовательно, новые координаты фокусов:

Из формул параллельного переноса найдем старые координаты фокусов:

, .

В старой системе координат фокусы гиперболы: и

Для того чтобы построить данную гиперболу, проведем старые и новые координаты оси. Отложим на осях и 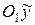в обе стороны от отрезки, равные двум единицам длины. Через полученные вершины гиперболы проведем ее основной прямоугольник (в данном случае – квадрат). Его диагонали являются асимптотами гиперболы. Далее, чертим ветви гиперболы, помня, что ее действительные вершины находятся на оси 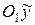. Для уточнения расположения гиперболы найдем точки ее пересечения со старыми координатными осями. Для этого полагаем в данном уравнении сначала а затем

, .

Рис. 3.5.4.

Корни первого уравнения комплексные, т.е. гипербола ось 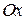не пересекает. Решая второе уравнение, найдем точки пересечения гиперболы с осью :

, .

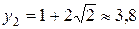Пример 3.5.5.. Привести к каноническому виду уравнение линии второго порядка . Определить вид и расположение линии, найти координаты фокуса. Сделать чертеж.

Решение. Так как член с отсутствует, то надо выделить полный квадрат только по :

Выносим также за скобку коэффициент при :

.

обозначаем или

Тем самым производится параллельной перенос системы координат в точку 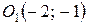. После переноса уравнение примет вид

или .

Отсюда следует, что данная линия есть парабола, точка 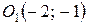является ее вершиной. Парабола направлена в отрицательную сторону оси и симметрична относительно этой оси (рис. ). Величина для нее равна , поэтому фокус имеет новые координаты:

.

Его старые координаты:

,

Если в данном уравнении положить или , то обнаружим, что парабола пересекает ось в точке , а ось 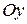она не пересекает.

Рис. .

Пример 3.5.6. Построить линию

.

Решение. Преобразуем уравнение к виду

,

.

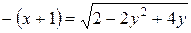(3.5.4)

Возведем обе части уравнения в квадрат:

При этом появились новые точки, которые не удовлетворяют уравнению (2.5.4). Эти посторонние точки отбросим потом. Выделим полный квадрат по :

,

то есть

Обе части разделим на 4 и произведем параллельный перенос системы координат: 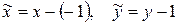. Получим уравнение

,

которое является каноническим уравнением эллипса с полуосями: 2 и . Центр эллипса находится в новом начале координат . Сделаем чертеж (рис. ).

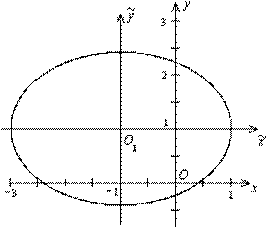
Рис. .

Чтобы отбросить посторонние точки, возникшие при возведении в квадрат, преобразуем уравнение (2.5.4) к виду

(3.5.5)

Из уравнения (2.5.5) ясно, что . Поэтому от полученного ранее эллипса следует оставить только левую половину (рис. ).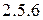

Рис. .

Рисунок и является ответом к примеру 3.5.6..

Пример 3.5.7. Записать уравнение гиперболы, фокусы которой находятся в точках 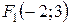, и полуось .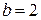

Решение. Фокусное расстояние . Полуоси 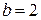, . Центр гиперболы находится на середине отрезка в точке с координатами . Точка имеет координаты . Следовательно, уравнение гиперболы .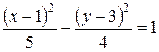

Ответ: .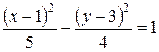

Пример 3.5.8. Записать уравнение параболы с фокусом и директрисой .

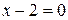Решение. Вершина параболы находится в точке , ордината которой равна ординате фокуса, т.е . Так как вершина равноудалена от фокуса и директрисы, то . при этом . Фокус лежит правее директрисы. Поэтому парабола направлена ветвями вправо. Запишем уравнение параболы: .

Ответ: .

Пример 3.5.9. Выяснить геометрический смысл уравнения .

Решение. Дополнив левую часть до полных квадратов, имеем:

,

т.е. .

Представление левой части в виде разности квадратов приводит к уравнению

или

.

Это уравнение эквивалентно паре линейных уравнени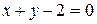й и . Таким образом, исходное уравнение выражает пару прямых, пересекающихся в точке .

Ответ: прямые 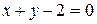, , пересекающиеся в точке .

Дата добавления: 2015-07-20