
Читайте также:
|
Найти координаты фокусов эллипса:
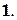
 .
.

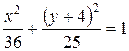 .
.

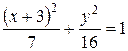 .
.
Написать уравнение эллипса с фокусами в точках  ,
,  и большой полуосью, равной
и большой полуосью, равной  :
:


 и большой полуосью, равной
и большой полуосью, равной  .
.

 и большой полуосью, равной
и большой полуосью, равной  .
.

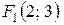
 и большой полуосью, равной
и большой полуосью, равной  .
.
Найти полуоси и координаты фокусов гиперболы:

 .
.

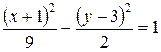 .
.

 .
.

 .
.
Написать уравнение гиперболы, фокусы которой в точках  ,
,  и действительная полуось
и действительная полуось  :
:


 ,
,  .
.


 ,
,  .
.
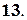
 ,
,  .
.
Написать уравнение асимптот гиперболы:

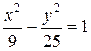 .
.

 .
.
 .
.

 .
.
Построить кривые:

 .
.
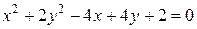 .
.
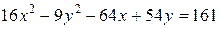 .
.

 .
.

 .
.

 .
.
 Выяснить геометрический смысл уравнения
Выяснить геометрический смысл уравнения  .
.
Ответы:
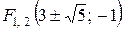 .
. 
 .
. 
 .
.

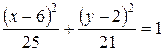 .
. 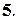
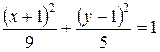 .
. 
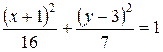 .
.

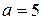 ,
, 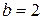 ,
,  .
. 
 ,
, 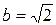 ,
,  .
.

 ,
,  ,
,  .
. 
 ,
, 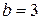 ,
,  .
.

 .
. 
 .
. 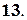
 .
. 
 ,
, 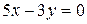 .
. 
 ,
,  .
.
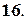
 ,
,  .
. 
 ,
,  .
.

 .
. 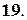
 .
. 
 .
. 
 .
. 
 .
. 
 .
. 
 – пустое множество точек, т.к. левая часть уравнения неположительна, а правая равна
– пустое множество точек, т.к. левая часть уравнения неположительна, а правая равна  . Можно назвать это множество точек мнимым эллипсом с полуосями
. Можно назвать это множество точек мнимым эллипсом с полуосями  и
и  .
.
Вопросы для самопроверки
1. Сформулируйте определение окружности.
2. Напишите каноническое уравнение окружности.
3. Сформулируйте определение эллипса.
4. Запишите каноническое уравнение эллипса.
5. Что такое полуоси эллипса?
6. Что называется эксцентриситетом эллипса? Что характеризует эксцентриситет эллипса и какова его величина?
7. Чему равен эксцентриситет окружности?
8. Сколько осей симметрии имеет эллипс?
9. Сформулируйте определение гиперболы.
10. Какая кривая называется гиперболой?
11. Запишите каноническое уравнение гиперболы.
12. Запишите уравнение равносторонней гиперболы.
13. Сколько осей симметрии имеет гипербола?
14. Что такое асимптоты гиперболы? Сколько асимптот имеет гипербола?
15. Каковы основные свойства гиперболы?
16. Сформулируйте определение параболы.
17. Запишите каноническое уравнение параболы.
18. Что называется параметром параболы? Можно ли, зная параметр параболы, найти ее расстояние от фокуса до вершины?
19. Сколько осей симметрии имеет парабола?
20. Как приводится общее уравнение линии второго порядка к каноническому виду?
21. Напишите формулу преобразования координат при параллельном переносе системы координат.
Дата добавления: 2015-07-20; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Параллельный перенос осей координат | | | В ноябре 1942 года мы эвакуировались. В августе 1944 вернулись в Ленинград |