Сигналов

7.1. Разложение периодических сигналов

по ортогональным функциям

Электрический сигнал 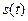(ток или напряжение ) называют периодическим, если он существует на интервале времени от 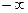до 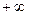и удовлетворяет условию , где 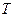- период сигнала, а - целое число. Примеры таких функций времени показаны на рис. 7.1.

Рис. 7.1

При расчете разнообразных сигналов удобно представить их взвешенной суммой заданных функций времени вида

, (7.1)

где - заданный набор (базис) функций времени, - весовые коэффициенты, не зависящие от времени. В этом случае функция времени 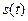может описываться набором коэффициентов 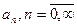, от времени не зависящих.

Чтобы разложение в ряд (7.1) было взаимно однозначным

функции должны быть взаимно ортогональными на периоде сигнала, то есть должны удовлетворять условию

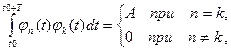(7.2)

где момент начала интегрирования 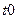выбирается произвольно исходя из удобства расчетов. При набор функций называют ортонормальным.

Для ортогонального базиса коэффициенты разложения определяются выражением

. (7.3)

В математике и технике широко используются различные ортогональные наборы функций (базисы) и прежде всего гармонический базис

, (7.4)

полиномы Чебышева, Лагранжа, Эрмита и др. В цифровой технике применяют ортогональные дискретные функции Уолша, Радамахера.

7.2. Ряд Фурье

Ряд Фурье для действительной периодической функции времени 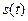является ее разложением по ортогональному базису (7.4) и имеет вид

(7.5)

Компоненту ряда Фурье вида

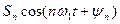(7.6)

называют 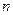-й гармоникой сигнала,

(7.7)

- частота первой гармоники, - постоянная составляющая сигнала,

, (7.8)

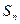- амплитуда 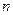-й гармоники сигнала,

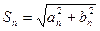, (7.9)

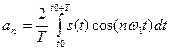, (7.10)

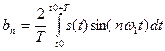, (7.11)

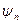- начальная фаза 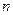-й гармоники сигнала,

(7.12)

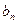Величины и называют амплитудами синфазной и квадратурной составляющих 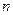-й гармоники сигнала соответственно.

7.3. Спектры амплитуд и фаз периодического сигнала

Периодический сигнал 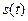взаимно однозначно описывается суммой гармоник

, (7.13)

то есть двумя в общем случае бесконечными наборами чисел.

Первый из них называют спектром амплитуд сигнала,

, (7.14)

а второй – спектром фаз,

. (7.15)

Спектры амплитуд и фаз не зависят от времени, а определяются формой сигнала 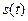на периоде колебаний. Частоты гармоник 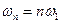кратны частоте первой гармоники ,

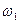, (7.16)

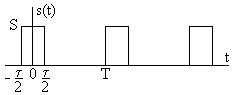
не зависят от формы сигнала и определяются только периодом его повторения .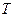

Спектры сигнала можно представить в виде формулы, таблицы или графика. В качестве примера рассмотрим спектры амплитуд и фаз последова-

Рис. 7.2 тельности прямоугольных

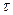импульсов с амплитудой , длительностью и периодом 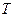, показанных на рис. 7.2. При расчетах целесообразно выбрать момент начала интегрирования 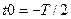. Постоянная составляющая равна

, (7.17)

а амплитуды синфазной и квадратурной составляющих -

, (7.18)

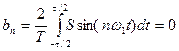. (7.19)

Для амплитуды и начальной фазы 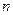-й гармоники получим

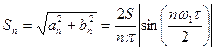, (7.20)

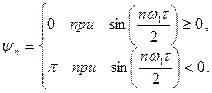(7.21)

Графики спектров амплитуд и фаз при условии , мс, мс показаны на рис. 7.3а и рис. 7.3б соответственно. Каждая гармоника отображается вертикальной линией, длина которой равна величине амплитуды или фазы.

Рис. 7.3

Переменная 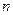является номером гармоники. Ее можно рассматривать как нормированную частоту гармоники,

,

и спектральные диаграммы можно строить в координатах частоты гармоники, как показано на рис. 7.4 для спектра амплитуд.

Спектры имеют дискретный (линейчатый) характер, интервал частот между соседними гармониками одинаков и

Дата добавления: 2015-07-25