
2.1 Системы параметров четырехполюсника
В ряде случаев необходимо не описать свойства четырехполюсника в виде частотных характеристик, а сформировать его модель, связывающую между собой входные и выходные токи и напряжения. Аналогичные модели уже использовались при описании двухполюсных элементов, которые характеризуются двумя переменными – протекающим током и приложенным к элементу напряжением. Например, модель «сопротивление» имеет вид  .
.
У четырехполюсника вида рис. 1.2 четыре переменных – входной 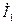 и выходной
и выходной 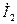 токи, входное
токи, входное 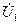 и выходное
и выходное 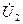 напряжения. Любые две из них можно выбрать в качестве независимых, тогда две оставшихся будут зависимыми. В результате модель будет представлять собой систему из двух линейных алгебраических уравнений.
напряжения. Любые две из них можно выбрать в качестве независимых, тогда две оставшихся будут зависимыми. В результате модель будет представлять собой систему из двух линейных алгебраических уравнений.
Всего возможно построить
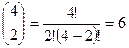
моделей, где 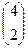 - число сочетаний из четырех переменных по две.
- число сочетаний из четырех переменных по две.
Если в качестве независимых переменных выбрать входное 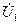 и выходное
и выходное 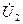 напряжения, то модель можно записать в виде
напряжения, то модель можно записать в виде
 . (2.1)
. (2.1)
Модель полностью характеризуется четырьмя коэффициентами ( ,
,  ,
,  ,
, 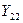 ) и поэтому ее называют системой Y-параметров. Все Y-параметры являются комплексными проводимостями, зависят от схемы и параметров элементов четырехполюсника, а также частоты сигнала. Систему уравнений (2.1) можно записать в матричной форме:
) и поэтому ее называют системой Y-параметров. Все Y-параметры являются комплексными проводимостями, зависят от схемы и параметров элементов четырехполюсника, а также частоты сигнала. Систему уравнений (2.1) можно записать в матричной форме:
 , (2.2)
, (2.2)
В этом случае модель полностью определяется матрицей Y-параметров:
 . (2.3)
. (2.3)
Выбрав независимыми переменными входной ток 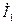 и выходное напряжение
и выходное напряжение 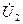 , получим модель четырехполюсника в виде системы H-параметров:
, получим модель четырехполюсника в виде системы H-параметров:
 , (2.4)
, (2.4)
или в матричной форме
 , (2.5)
, (2.5)
где матрица H-параметров имеет вид
 . (2.6)
. (2.6)
Параметр  имеет размерность сопротивления,
имеет размерность сопротивления,  и
и  - безразмерны, а
- безразмерны, а  является проводимостью. В общем случае это комплексные величины, зависящие от схемы и параметров элементов четырехполюсника, а также от частоты сигнала.
является проводимостью. В общем случае это комплексные величины, зависящие от схемы и параметров элементов четырехполюсника, а также от частоты сигнала.
Используются и другие системы параметров, которые представлены в табл. 2.1.
Таблица 2.1
| Система параметров | Система уравнений | Матричная форма |
| Z | 
| 
|
| A | 
| 
|
| B | 
| 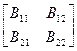
|
| F | 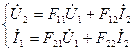
| 
|
Штрих в обозначении токов указывает на их противоположное направление по сравнению с указанным на рис. 1.2. Все шесть рассмотренных моделей описывают свойства одной и той же цепи, следовательно, они эквивалентны и одна система параметров может быть определена через другую. В литературе [2, приложение 15] имеются соответствующие формулы пересчета параметров из одной системы в другую.
2.1. Физический смысл параметров четырехполюсника
Проведем анализ системы H-параметров четырехполюсника. Уравнения имеют вид (2.4) и применимы для любых значений независимых переменных ( и
и  ).
).
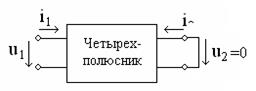 Допустим, что выходное напряжение
Допустим, что выходное напряжение 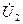 равно нулю. Физически это условие можно обеспечить при коротком замыкании выхода четырехполюсника, как показано на рис. 2.1. При этом из
равно нулю. Физически это условие можно обеспечить при коротком замыкании выхода четырехполюсника, как показано на рис. 2.1. При этом из
Рис. 2.1 первого уравнения сис-
темы (2.4) получим
 . (2.7)
. (2.7)
Как видно, параметр  , равный отношению входного напряжения к входному току, является комплексным входным сопротивлением четырехполюсника при коротком замыкании выхода и измеряется в Омах.
, равный отношению входного напряжения к входному току, является комплексным входным сопротивлением четырехполюсника при коротком замыкании выхода и измеряется в Омах.
Из второго уравнения системы (2.4) можно записать
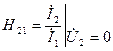 , (2.8)
, (2.8)
то есть  представляет собой безразмерный комплексный коэффициент передачи тока при коротком замыкании выхода.
представляет собой безразмерный комплексный коэффициент передачи тока при коротком замыкании выхода.
Допустим, что входной ток четырехполюсника 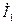 равен нулю, что соответствует холостому ходу (разрыву) входной цепи, как показано на рис. 2.2.
равен нулю, что соответствует холостому ходу (разрыву) входной цепи, как показано на рис. 2.2.
 Из первого уравнения системы (2.4) получим
Из первого уравнения системы (2.4) получим
 (2.9)
(2.9)
Как видно, параметр Рис. 2.2
 равен отношению
равен отношению
комплексных амплитуд входного и выходного напряжений. Его целесообразно назвать комплексным коэффициентом обратной передачи напряжения при холостом ходе входной цепи.
Из второго уравнения (2.4) следует
 , (2.10)
, (2.10)
то есть  является комплексной выходной проводимостью четырехполюсника при холостом ходе входной цепи.
является комплексной выходной проводимостью четырехполюсника при холостом ходе входной цепи.
Рассмотрим систему Y-параметров на основе уравнений (2.1). Допустим, что  (обеспечен режим короткого замыкания выхода), тогда параметр
(обеспечен режим короткого замыкания выхода), тогда параметр
 (2.11)
(2.11)
представляет собой комплексную входную проводимость, а
 (2.12)
(2.12)
- комплексную проходную проводимость четырехполюсника при коротком замыкании выхода.
Аналогично при  (обеспечен режим короткого замыкания входа)
(обеспечен режим короткого замыкания входа)
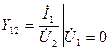 (2.13)
(2.13)
является комплексной приводимостью обратной передачи,
 (2.14)
(2.14)
- комплексной выходной проводимостью при коротком замыкании входа четырехполюсника.
Как уже отмечалось, системы параметры зависят от схемы и параметров элементов четырехполюсника и от частоты входного сигнала.
Полученные выражения (2.7) - (2.10) не только выявляют физический смысл параметров, но позволяют сформировать методики их расчета и измерения.
 |
2.3. Методика расчета параметров четырехполюсников
В качестве примера рассмотрим расчет H-параметров четырехполюсника, схема которого показана на рис. 2.3а.
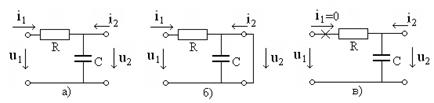
Рис. 2.3
 Обеспечим режим короткого замыкания выхода, как показано на рис. 2.3б, и, полагая известным входное напряжение
Обеспечим режим короткого замыкания выхода, как показано на рис. 2.3б, и, полагая известным входное напряжение 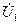 , любым методом расчета найдем входной ток
, любым методом расчета найдем входной ток 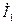 , В цепи рис. 2.3б емкость
, В цепи рис. 2.3б емкость 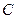 замкнута, схема принимает вид, показанный на рис. 2.4, тогда по закону Ома
замкнута, схема принимает вид, показанный на рис. 2.4, тогда по закону Ома
 ,
,
а из (2.7) получим
Рис. 2.4
 .
.
Затем, полагая известным входной ток 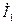 , любым методом определим выходной ток
, любым методом определим выходной ток 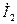 . В цепи на рис. 2.4 очевидно, что
. В цепи на рис. 2.4 очевидно, что  , тогда из (2.8) следует
, тогда из (2.8) следует
 .
.
Далее обеспечиваем режим холостого хода входной цепи, как показано на рис. 2.3в. При  напряжение на сопротивлении
напряжение на сопротивлении 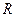 равно нулю. Полагая известным выходное напряжение
равно нулю. Полагая известным выходное напряжение 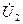 , любым методом определим входное напряжение
, любым методом определим входное напряжение
 . Для цепи рис. 2.3в получим
. Для цепи рис. 2.3в получим  , тогда из (2.9)
, тогда из (2.9)
 .
.
Затем при заданном выходном напряжение 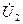 любым методом определим выходной ток
любым методом определим выходной ток 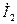 . В рассматриваемом случае в выходной цепи включена только емкость
. В рассматриваемом случае в выходной цепи включена только емкость 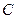 (сопротивление
(сопротивление 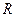 отключено), тогда
отключено), тогда 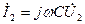 и из (2.10) получим
и из (2.10) получим
 .
.
В результате матрица H-параметров равна
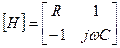 ,
,
а система уравнений (модель) принимает вид

Как видно, первое уравнение модели соответствует уравнению второго закона Кирхгофа, а второе уравнение – уравнению первог о закона Кирхгофа для цепи рис. 2.3а. Этот результат является частным случаем, и обусловлен простотой цепи, показанной на рис. 2.3а.
Определим систему Y-параметров того же четырехполюсника на рис. 2.3а. В режиме короткого замыкания выхода (рис. 2.3б и рис. 2.4) получим
 ,
,
 .
.
 Обеспечим режим короткого замыкания входной цепи, как показано на рис. 2.5, при этом
Обеспечим режим короткого замыкания входной цепи, как показано на рис. 2.5, при этом
 ,
,
 .
.
В результате получим матрицу Рис. 2.5
Y-параметров
 ,
,
и систему уравнений в виде


2.4. Измерение параметров четырехполюсников
На практике часто приходится иметь дело с электронными устройствами, которые можно рассматривать как линейные четырехполюсники. Прежде всего, это пассивные  цепи, например, частотные фильтры. Однако и устройства, содержащие нелинейные элементы (например, транзисторные усилители) можно рассматривать как линейные четырехполюсники, если воздействующие на них переменные сигналы достаточно малы (режим малого сигнала в усилителе).
цепи, например, частотные фильтры. Однако и устройства, содержащие нелинейные элементы (например, транзисторные усилители) можно рассматривать как линейные четырехполюсники, если воздействующие на них переменные сигналы достаточно малы (режим малого сигнала в усилителе).
Если устройство работает в линейном режиме, то, измерив его систему параметров, можно построить простую и удобную в использовании экспериментальную модель.
Параметры линейного четырехполюсника могут быть измерены с использованием соотношений, подобных (2.7)-(2.10) для H-параметров. В этом случае необходимо реализовать эксперименты (опыты) короткого замыкания выхода и холостого хода входа, как показано на рис. 2.6 применительно к модулям H-параметров.
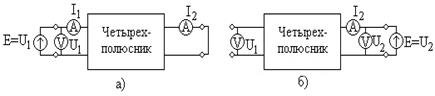
Рис. 2.6
При коротком замыкании выхода (рис. 2.6а) к нему вместо нагрузки подключается перемычка, а к входу – генератор гармонического сигнала с заданной частотой и ЭДС  . По показаниям вольтметра и амперметров в цепи рис. 2..6а измеряются действующие значения входного напряжения
. По показаниям вольтметра и амперметров в цепи рис. 2..6а измеряются действующие значения входного напряжения  , входного
, входного  и выходного
и выходного  токов, тогда получим
токов, тогда получим
 ,
,  . (2.15)
. (2.15)
В режиме холостого хода входной цепи (рис. 2.6б) генератор подключается к выходу четырехполюсника и измеряются действующие значения выходного тока  , входного
, входного  и выходного
и выходного  напряжений, тогда
напряжений, тогда
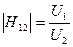 ,
, 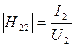 . (2.16)
. (2.16)
Если необходимо определить комплексные значения H-параметров, то потребуется измерение их аргументов, которое можно осуществить с помощью двулучевого осциллографа (рис. 2.7). Для этого в ветви с измеряемым током вместо амперметров включаются резисторы с малым сопротивлением  и падения напряжения на них (
и падения напряжения на них ( или
или  ) при необходимости подаются на осциллограф. По смещению во времени двух сравниваемых гармонических сигналов измеряется сдвиг фаз между ними (например, при измерении аргумента
) при необходимости подаются на осциллограф. По смещению во времени двух сравниваемых гармонических сигналов измеряется сдвиг фаз между ними (например, при измерении аргумента 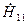 в схеме на рис. 2.7а на осциллограф подаются напряжения
в схеме на рис. 2.7а на осциллограф подаются напряжения  и
и  ).
).

Рис. 2.7
Промышленность выпускает измерительные приборы, позволяющие экспериментально определять, например, H-параметры биполярных транзисторов. Эта возможность преду-
сматривается даже в некоторых бытовых мультиметрах (малогабаритных простых приборах для измерения токов, напряжений и сопротивлений).

При измерении параметров четырехполюсников эксперименты короткого замыкания и холостого хода, особенно выходной цепи, необходимо проводить инженерно грамотно. В противном случае можно вывести измеряемое устройство (усилитель) из строя.
2.5. Соединения четырехполюсников
Для двухполюсников имеется два простых варианта их соединения – последовательное и параллельное. У четырехполюсников таких простых вариантов соединения уже пять, как показано на рис. 2.8:
- последовательное по входу и выходу (рис. 2.8а);
- параллельное по входу и выходу (рис. 2.8б);
- последовательное по входу и параллельное по выходу
(рис. 2.8в);
- параллельное по входу и последовательное по выходу
(рис. 2.8г);
- каскадное (рис. 2.8д).
Каждое соединение можно представить одним эквивалентным четырехполюсником, что дает возможность преобразовывать сложные соединения четырехполюсников, представляя их простыми моделями.
Матрицу параметров эквивалентного четырехполюсника можно выразить через матрицы параметров двух входящих в соединение четырехполюсников в соответствии с табл. 2.2.
Простые выражения (табл. 2.2) имеют место при определенном выборе системы параметров в зависимости от характера соединения четырехполюсников, поэтому на практике широко используются все системы параметров. Если при описании входящих в соединение четырехполюсников использовать другие системы параметров, то выражение для эквивалентных параметров существенно усложняются [2].
Соотношения из табл. 2.2 позволяют существенно упростить расчеты сложных цепей, которые можно представить как соединение простых четырехполюсников.


Рис. 2.8
Таблица 2.2
| Вид соединения | Матрица |
| Последовательное по входу и выходу | 
|
| Параллельное по входу и выходу | 
|
| Последовательное по входу и параллельное по выходу | 
|
| Параллельное по входу и последовательное по выходу | 
|
| Каскадное | 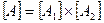
|
В качестве примера рассмотрим цепь, схема которой показана на рис. 2.9. Ее можно рассматривать как отдельный четырехполюсник, или как каскадное соединение двух четырехполюсников со схемой, показанной на рис. 2.5.

Рис. 2.9
Определим матрицу A-параметров четырехполюсника на рис. 2.9., уравнения которого имеют вид
 . (2.17)
. (2.17)
Обеспечим в цепи режим короткого замыкания выхода  , схема цепи
, схема цепи
Рис. 2.10 показано на рис. 2.10.
Найдем параметры 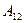 и
и  , равные
, равные
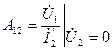 ,. (2.18)
,. (2.18)
 . (2.19)
. (2.19)
Для этого при известном напряжении 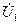 необходимо найти ток
необходимо найти ток  . По закону Ома ток
. По закону Ома ток 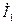 равен
равен
 ,
,
где  - сопротивление емкости, тогда для напряжения
- сопротивление емкости, тогда для напряжения 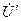 получим
получим
 ,
,
а для тока  соответственно
соответственно
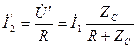 .
.
Для  можно записать выражение
можно записать выражение
 .
.
Подставляя в выражение для  ток
ток 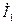 , получим
, получим
 ,
,
в результате параметр 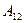 будет равен
будет равен
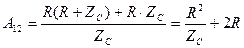 .
.
Обеспечим режим холостого хода выхода 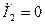 в цепи на рис. 2.9. В этом случае можно определить
в цепи на рис. 2.9. В этом случае можно определить
 , (2.20)
, (2.20)
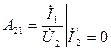 . (2.21)
. (2.21)
Для цепи рис. 2.9 можно записать
 ,
,
 ,
,
тогда выходное напряжение будет равно
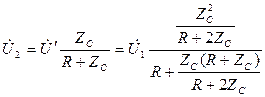 ,
,
а для параметра  получим
получим
 ,
,
Зная ток 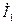 , запишем выражение для выходного напряжения
, запишем выражение для выходного напряжения 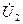 ,
,
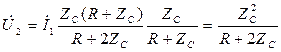 ,
,
тогда параметр  будет равен
будет равен
 .
.
Расчет A-параметров четырехполюсника на рис. 2.9 можно провести значительно проще, если представить его каскадным соединением двух более простых четырехполюсников, показанных на рис. 2.11а, схема цепи в режиме короткого замыкания выхода приведена на рис. 2.11б..

Рис. 2.11
Проведите расчет системы A-параметров четырехполюсника рис. 1.11а самостоятельно. В результате нетрудно получить
 .
.
Матрица A-параметров четырехполюсника на рис. 2.6  равна произведению двух матриц
равна произведению двух матриц  ,
,
 ,
,
в результате получим
 .
.
Как видно, расчет каскадного соединения существенно проще, чем исходной цепи на рис. 2.9.
2.6. Параметры четырехполюсника и его частотные
характеристики
Подключим к четырехполюснику источник сигнала с ЭДС  и внутренним сопротивлением
и внутренним сопротивлением  и нагрузку
и нагрузку  . Для описания четырехполюсника используем систему A-параметров. В результате на основе законов Ома и Кирхгофа получим систему уравнений вида
. Для описания четырехполюсника используем систему A-параметров. В результате на основе законов Ома и Кирхгофа получим систему уравнений вида

Рис. 2.12
 (2.22)
(2.22)
При известной ЭДС источника и параметрах элементов цепи из системы уравнений (2.22) можно определить все токи и напряжения.
Из уравнений (2.23) можно определить комплексный коэффициент передачи напряжения в виде
 . (2.23)
. (2.23)
Из второго уравнения (2.22) можно записать
 , (2.24)
, (2.24)
тогда комплексный коэффициент передачи тока равен
 . (2.25)
. (2.25)
Как видно, частотные характеристики нагруженного четырехполюсника определяются его A-параметрами и сопротивлением нагрузки. При отсутствии нагрузки ( ) из (2.23) получим
) из (2.23) получим
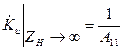 . (2.26)
. (2.26)
В качестве примера рассмотрим цепь на рис. 2.13, для которой нетрудно показать, что
 .
.

Рис. 2.13
С другой стороны, из (2.23) при известных A-параметрах четырехполюсника рис. 2.11а получим
 .
.
Как видно, полученные выражения для 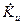 полностью совпадают.
полностью совпадают.
2.7. Применение моделей четырехполюсников
Модели четырехполюсников и их системы параметров широко используются в различных областях электротехники и электроники.
Это прежде всего теория линейных четырехполюсных трактов передачи сигналов, трансформации напряжений, токов, мощности и сопротивлений, задачи анализа и синтеза частотных фильтров с заданными частотными характеристиками.
Системы параметров четырехполюсников применяются для описания нелинейных активных элементов (транзисторов) в режиме малого сигнала. Для описания биполярных транзисторов чаще всего используется система H-параметров. В справочниках по транзисторам их усилительные свойства определяются статическим (определяемом на постоянном токе) коэффициентом передачи тока в схеме с общим эмиттером  , который является соответствующим H-параметром.
, который является соответствующим H-параметром.
Для измерения всех H-параметров биполярных транзисторов имеются специальные измерительные приборы. Даже некоторые бытовые мультиметры (универсальные измерители напряжения, тока и сопротивления) имеют возможность измерения параметра  . Все это свидетельствует о широком практическом применении этой системы параметров. В описа-
. Все это свидетельствует о широком практическом применении этой системы параметров. В описа-
нии полевых транзисторов и электронных ламп применяют систему Y-параметров. Статический параметр 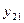 имеет специальное название крутизны.
имеет специальное название крутизны.
При разработке малосигнальных моделей полупроводниковых приборов часто используется система Z-параметров.
2.8. Задания для самостоятельного решения
Задание 1.1. Определите системы Y-параметров и H-параметров четырехполюсников, схемы которых показаны на рис. 2.14. Повторите расчеты, заменив емкость C на индуктивность L. Представьте результаты в виде частотных характеристик

Рис. 2.14
Задание 1.2. Определите систему A-параметров четырехполюсников, схемы которых показаны на рис. 2.15. Представьте результаты в виде частотных характеристик

Рис. 2.15
Дата добавления: 2015-07-25; просмотров: 148 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Фазочастотная характеристика (ФЧХ) – это зависимость от частоты аргумента комплексного коэффициента передачи. Она представляет собой сдвиг фаз между выходным и входным сигналами. | | | ЧАСТОТНЫХ ФИЛЬТРОВ |