Дискретные случайные величины

Рассмотрим подробнее дискретные случайные величины, причем, как правило, будем ограничивать рассмотрение такими случай­ными величинами, у которых количество возможных значений конечно.

Наиболее полную информацию о дискретной случайной вели­чине дает закон распределения этой величины.

Определение. Законом распределения дискретной случайной величины называется соответствие между всеми возможными значениями этой случайной величины и соответствующими им вероятностями.

Закон распределения дискретной случайной величины часто задают в виде двухстрочной таблицы, в первой строке которой перечислены все возможные значения этой величины (как правило, в порядке возрастания), а во второй — соответствующие этим значениям вероятности таблице 1:

X	X1	X2	…	Xn
P	P1	P2	…	Pn

Пример 2. Имеется десять студенческих групп, насчитыва­ющих соответственно 12, 10, 11, 8, 12, 9, 10, 8, 10 и 11 студентов. Составить закон распределения случайной величины X, опреде­ляемой как число студентов в наугад выбранной группе.

Решение. Возможными значениями рассматриваемой случай­ной величины Х являются следующие (в порядке возрастания):

8, 9, 10, 11 и 12.

Поскольку случайная величина Х принимает значение, равное 8, в том случае, если наугад выбранной группой окажется груп­па из 8 студентов (назовем это событием А), вероятность того, что случайная величина Х примет значение 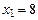, равна вероят­ности этого случайного события: .

Вероятность же случайного события А в соответствии с классическим определением вероятности равна по­скольку из 10 групп две насчитывают по 8 студентов.

Таким образом, для вероятности значения 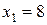получаем:

.

Аналогично можно найти вероятности остальных значений слу­чайной величины X:

что позволяет составить искомый закон распределения (таблица 2):

X
P	0,2	0,1	0,3	0,2	0,2

Закон распределения дискретной случайной величины может быть задан также с помощью формулы, позволяющей для каж­дого возможного значения этой величины определить соответ­ствующую вероятность.

Дата добавления: 2015-07-25