Основные числовые характеристики непрерывной случайной величины

Под основными числовыми характеристиками непрерывной слу­чайной величины понимают, как и в случае дискретной случай­ной величины, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Как и для дискретной величины, математическое ожидание представляет собой среднее значение этой величины, а дисперсия и среднее квадратическое отклонение являются усредненными характеристиками степени разброса возможных значений этой величины относительно ее математического ожидания.

Однако формулы, определяющие математическое ожидание и дисперсию непрерывной случайной величи­ны, отличаются от соответствующих формул для дискретной ве­личины и в общем случае имеют соответственно вид:

, (6)

, (7)

Среднее квадратичное отклонение, как и для дискретной случайной величины, определяется формулой:

, (8)

Нормальный закон распределения (закон Гаусса)

Из известных видов распределения непрерывных случайных ве­личин наиболее часто используют нормальное распределение, опи­сываемое законом Гаусса. Это объясняется как его относитель­ной простотой, так и тем, что многие случайные величины, фор­мирование значений которых определяется большим количеством неконтролируемых факторов, каждый из которых вносит относи­тельно небольшой вклад, имеют распределение, близкое к нормальному.

Определение. Непрерывная случайная величина называется распределенной по нормальному закону (закону Гаусса), если ее плотность вероятности имеет вид

, (9)

где 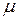—математическое ожидание; — дисперсия; — среднее квадратическое отклонение этой величины.

График плотности вероятности нормального закона распреде­ления (кривая Гаусса) приведен на рис. 1.

Этот график симметричен относительно вертикальной прямой 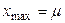причем в точке функция имеет максимум, рав­ный .

Поскольку при функция f(х) стремится к 0, то ось абсцисс является асимптотой графика этой функции.

Рисунок 1. График плотности вероятности нормального закона распреде­ления (кривая Гаусса)

Дата добавления: 2015-07-25