Основные числовые характеристики дискретной случайной величины

Как уже отмечалось, закон распределения дискретной случайной величины позволяет получить исчерпывающую информацию об этой величине.

На практике закон распределения изучаемой величины часто неизвестен, но даже и в тех случаях, когда он известен, для описания определенных особенностей этой величины используют ее так называемые основные числовые характеристики, из ко­торых рассмотрим математическое ожидание, дисперсию и сред­нее квадратическое отклонение (стандарт).

Определение. Математическим ожиданием М(Х) (часто ис­пользуется также обозначение «») дискретной случайной ве­личины Х называется сумма произведений каждого из всех ее возможных значений на соответствующие вероятности:

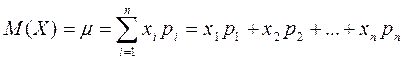, (3)

где индекс i принимает значения 1, 2, 3,..., п.

Пример 3. Вычислить математическое ожидание дискретной случайной величины X, определяемой как количество студентов в наугад выбранной группе, используя данные табл. 2 (см. при­мер 2).

Решение. Подставляя данные табл. 8.3 в формулу (3), по­лучим:

Основной смысл математического ожидания дискретной слу­чайной величины состоит в том, что оно представляет собой среднее значение данной величины. Иными словами, если произведено некоторое количество испытаний и по результатам этих испыта­ний вычислено среднее арифметическое всех наблюдавшихся значений дискретной случайной величины X, то это среднее ариф­метическое значение приближенно равно (тем точнее, чем больше количество испытаний) математическому ожиданию данной слу­чайной величины.

Для характеристики степени разброса возможных значений дискретной случайной величины относительно ее математическо­го ожидания вводят понятие дисперсии дискретной случайной величины.

Определение. Дисперсией D(X) (часто используется также обо­значение «») дискретной случайной величины, называется ма­тематическое ожидание квадрата отклонения этой величины от ее математического ожидания:

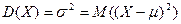, (4)

Дата добавления: 2015-07-25