Графические изображения рядов распределений случайной величины, их назначение и правила построения

Статистические графики – это условные изображения статистических данных в виде точек, линий или фигур.

В статистике графики используются:

- во-первых, для обобщения и анализа статистических данных. Графические изображения служат одним из важнейших технических и познавательных средств статистики;

- во-вторых, в целях широкой популяризации данных и для облегчения их восприятия не специалистами.

Несмотря на большое разнообразие статистических графиков, можно указать некоторые общие правила их построения.

При построении графика важно найти такие способы изображения, которые наилучшим образом отвечают содержанию и логической природе изображаемых показателей. Необходимо помнить, что никакой график не заменяет собой статистических данных. Поэтому, если на самом графике числа не написаны (это целесообразно делать только при условии, что они чрезмерно не загромоздят изображение), то они должны быть приведены в тексте.

График должен быть точным, построенным в соответствии с масштабом и т.п. Должна быть обеспечена полная возможность "чтения графика": наличие масштаба, объяснения смысла расцветок или штриховок, названий показателей, отвечающих тем или иным размерам на графике, и т.д. График не должен быть перегружен материалом. Если, например, линиями на одном графике изображается динамика нескольких показателей и нельзя избежать их переплетения, то изображать совместно динамику больше чем трех-четырех показателей (например, линиями разного цвета) уже нецелесообразно.

Дискретные группированные ряды распределений изображаются в виде линейной диаграммы – полигона. При его построении на оси абсцисс наносят значения случайной величины, а на оси ординат – абсолютные или относительные повторяемости (частоты, вероятности). Полученные точки соединяются затем отрезками прямых линий.

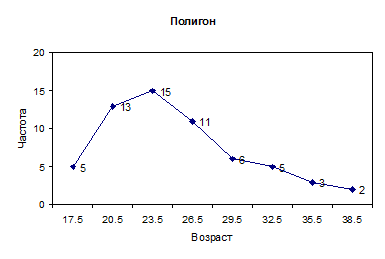
Гистограмма распределения применяется для изображения интервальных рядов. Для ее построения на оси абсцисс откладывают интервалы (градации) случайной величины, а на оси ординат –частоты или вероятности градаций. На интервалах строят прямоугольники, высоты которых равны частотам или вероятностям соответствующих интервалов.

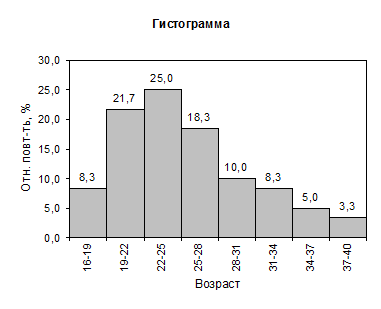
При использовании по оси абсцисс центральных значений случайной величины, а по оси ординат – величин относительных плотностей распределения получается дифференциальная кривая распределения интервального ряда.

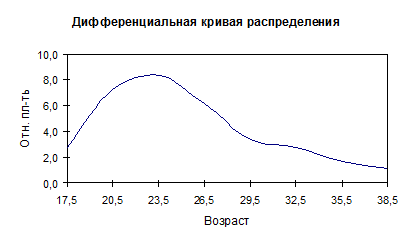
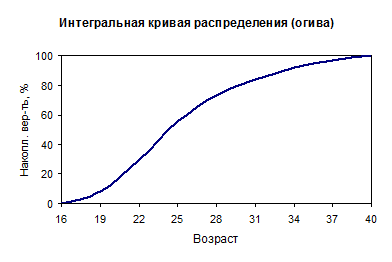
Для интервального ряда распределения также используется интегральная кривая распределения (ее еще называют кумулятивной кривой или огивой). Для ее построения на оси абсцисс откладывают все значения границ градаций от первой до последней, а на оси ординат – накопленные вероятности SР_i появления значений переменных, меньше соответствующей границы. Накопленные вероятности получают путем последовательного суммирования вероятностей для соответствующих градаций. По этим показателям легко определить, какова вероятность того, что случайная величина будет по величине меньше какого-то определенного уровня.

Свойства интегральной кривой распределения:

1). В точке, соответствующей самой нижней границе градаций, значение накопленной вероятности SР_i равно нулю, а в точке, соответствующей значению самой верхней границы градаций – SР_i = 100%, т.е. область построения кривой четко ограничена.

2). По характеру интегральная кривая является монотонно-неубывающей, т.е. она не может иметь минимумов.

Дата добавления: 2015-07-20