Самостійні домашні роботи

Кожний студент отримує індивідуальний варіант роботи, іноді поетапно. Завдання відповідають змісту модулів і розраховані на відпрацювання певних математичних операцій і дій, на закріплення означень і понять, властивостей і особливостей, а також мають місце і завдання творчого характеру. Після перевірки робіт, студенти мають можливість покращати результати шляхом роботи над помилками самостійно або за допомогою товаришів, які при умові позитивного результату теж отримують заохочуючу оцінку.

№	ДЗ №1	ДЗ №2	ДЗ №3
1.	Навести конкретні приклади до усих властивостей визначників і довести їх.	1.Дани координати вершин піраміди	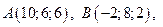1. Визначити ОДЗ функції: а)
2.	Довести властивість 9 для будь-яких стовпців (рядків) в загальному вигляді.	. Знайти: 1)довжину ребра АВ.	б) с)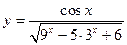
3.	Обчислити визначник (по будь-якому рядку(стовпцю) штучного доповнення, правило трикутника, правило Сарюса) - 4 способами:	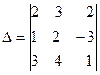2)Кут між ребрами АВ і АД.   3) Кут між ребром АД і гранню АВС.   4)Кут між гранями АВС та АДС.	2. Обчислити границі: 1) 2) 3)
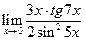
4.	Обчислити визначник будь-яким способом:	5) Площу грані АВС.   6) Об’єм піраміди.   7) Довжину висоти із Д на грань АВС.	4) 5) 6)
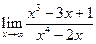
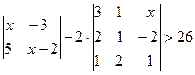
5.	Розв’язати нерівність:	8) Проекцію точки Д на грань АВС. Рівняння прямих: 9) Через вершину	7) 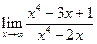8)
6.	Знайти А·В та В·А, якщо: А= , В =	С паралельно АД -ребру.   10) Через точку В перпендикулярно грані АДС.	9) 10)
7.	Знайти ранг матриці двома способами: А=	11) Скласти рівняння площини, що проходе через вершину С, перпендикулярно	3. Визначити неперервність функції:
8.	Розв’язати рівняння: 5А + 2Х – В = 0, якщо ,	ребру АВ.   12) Побудувати піраміду в просторі.	1) в точках х = 1 та х = 2.
9.	Знайти обернену матрицю двома способами:	2. Визначити та побудувати лінію, рівняння якої має вигляд: 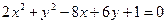.	2) f(x) = =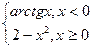
	Розв’язати систему лінійних алгебраічних рівнянь 3 способами (метод Гауса, правило Крамера, за допомогою оберненої матриці):	3. Дослідити лінійну залежність векторів: , .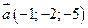
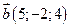4.Скласти рівняння ГМТ, для яких сума відстаней до точок А(2;3) і В(4;5)дорівнює 54.

3.2.2. Корекція самостійної роботи

Допомогти викладачеві організовувати і управляти самостійною

діяльністю студентів, здійснювати корекцію роботи студента на базі індивідуальних рекомендацій та завдань, з’ясувати питання про сформованість різних алгоритмічних прийомів розв’язування задач та основних розумових дій, що сприяють розвитку творчої діяльності, скоротити час на аналіз помилок у роботі можуть словники – таблиці, які розроблені студентами.

У процесі самостійного опрацювання нового матеріалу студенту

пропонується ряд запитань, на які він шукає відповіді у відповфдних підручниках та конспектах лекцій (трудомісткість 12 годин). У словнику - таблиці зазначається кожний логічний крок пошуку студента (табл.1).

Дата добавления: 2015-07-25