Примеры выполнения задач, по определению гидродинамических параметров взвешенного слоя

Задача 11. В аппарате имеется взвешенный слой силикагеля, ситовой состав которого следующий:

Фракция, d, мм.	2,0+1,5	1,5+1,0	1,0+0,5	0,5+0,25
Содержание х, % (масс.)

Насыпная плотность силикагеля плотность частиц Температура воздуха 150 Число псевдоожижения Определить критическую, рабочую и действительную (в свободном сечении между частицами) скорость воздуха.

Решение. Подсчитываем величину критерия Архимеда (Ar) и по рис. 3 находим соответствующее значение критерия Лященко C этой целью определяем эквивалентный диаметр частиц силикагеля.

Среднеситовые диаметры фракций:

Эквивалентный диаметр определяем по формуле 1.27:

Динамический коэффициент вязкости воздуха при 150 (приложение 2, таблица П.2.10).

Плотность воздуха при температуре 150 определяется по формуле:

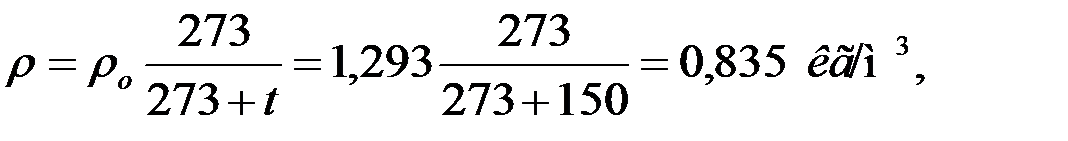(1.35).

Следовательно, критерий Архимеда (Аr), формула 1.4, будет равен:

Значению по графику (рис.1) соответствует Отсюда критическая скорость воздуха равна:

Определяем рабочую скорость воздуха, преобразовав уравнение 1.30:

Найдем порозность взвешенного слоя. Если в уравнение 1.30 вместо скоростей подставить уравнение 1.8 с соответствующими параметрами, то мы получим нижеприведенное уравнение и при

По рис. 3 при и имеем Действительная скорость воздуха в свободном сечении слоя, определяется по формуле 1.31.:

Задача 12. Определить диаметр шарообразных частиц кварцевого песка плотностью 2640 которые начнут переходить во взвешенное состояние при скорости потока воздуха 1 м/с и температуре воздуха 20

Решение. Диаметр шарообразных частиц песка определяем из уравнения критерия Архимеда (Ar), предварительно найдя значение критерия Лященко

где r_с – плотность воздуха при температуре 20^оС, определяется по формуле 1.35;

m_с – динамическая вязкость воздуха при температуре 20^оС, (приложение, таблица 2),

Значению соответствует, по рис. 3,

Искомый диаметр частиц песка, уравнение 1.11:

Задача 13. Во взвешенном слое содержится 1000 кг твердого материала; расход материала через слой (скорость ввода и вывода частиц) составляет 4000 кг/ч. Определить: какая доля частиц будет находиться в слое в течение времени, большего, чем среднее расходное время пребывания материала в слое.

Решение. Вычислим среднее расходное время пребывания материала в одном слое t _о , уравнение 1.33. При М = 1000 кг, L = 4000 кг/ч.

Определим долю материала, находящегося в одном взвешенном слое в течении времени

Таким образом, только 37% материала находится в слое больше 15 мин, и, следовательно, для материала, находящегося в слое, меньше 15 мин, составит:

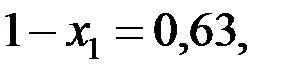т.е. 63%.

Дата добавления: 2015-07-11