Примеры выполнения задач, по определению параметров процесса осаждения

Задача 1. Найти верхний предел (наибольший диаметр частиц) применимости формул Стокса к частицам кварца плотностью 2650 осаждающимся в воде при температуре 20 ºС.

Решение.

Формула Стокса строго применима при Ar < 3,6. Поэтому наибольшая частица кварца, осаждение которой может быть рассчитано по формуле (1.11), должна иметь диаметр:

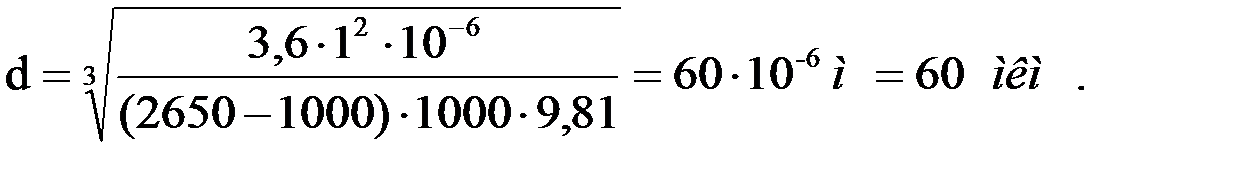
где , динамическая вязкость среды, для воды найдена при температуре 20 ºС в приложении 2, табл. П.2.1;

– плотность воды при 20 ºС (в приложении 2, табл. П.2.1)

Задача 2. Найти скорость осаждения в воде частиц кварцевого песка шарообразной формы диаметром 0,9 мм, если плотность песка 2650 а температура воды 20 ºС.

Решение.

Определяем критерий Архимеда (Ar) по формуле 1.3:

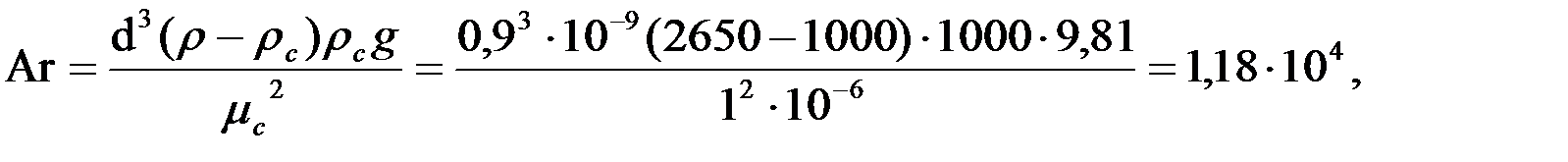
где , динамическая вязкость воды, в приложении 2, табл. П.2.1

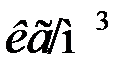, плотность воды, в приложении 2, табл. П.2.1

По значению 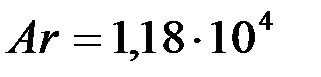по графику (рис. 1) находим Re = 140.

Тогда, скорость осаждения частиц кварцевого песка шарообразной формы диаметром 0,9 мм определяем из выражения 1.7.:

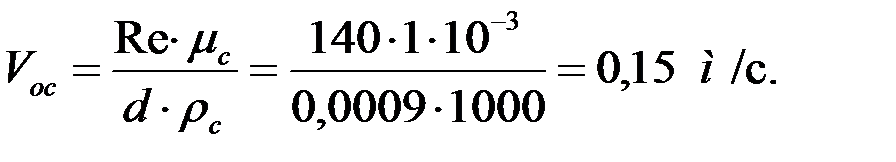
Задача 3. Определить размер наибольших шарообразных частиц мела, которые будут уноситься восходящем потоком воды, идущем со скоростью 0,5 м/c. Температура воды 10 ºС, плотность мела 2710

Решение. Определяем критерий Лященко (Ly) по формуле 1.5.:

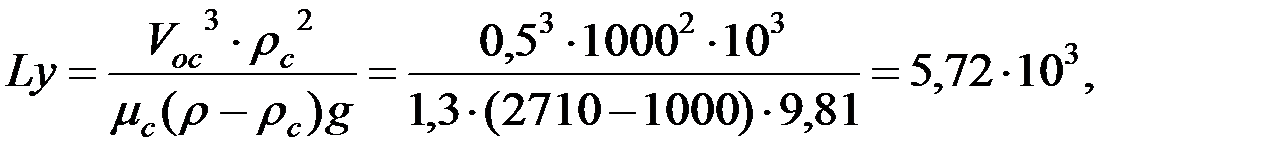
где 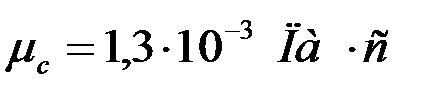, динамическая вязкость воды при температуре 10 ºС, в приложении 2, табл. П.2.1;

, плотность среды (в приложении 2, табл. П.2.1).

По найденному значению Ly = 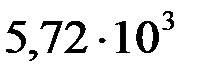из графика рис. 1 находим Re = 1750; затем определяем максимальный диаметр частиц мела, которые будут уноситься водой, преобразованная формула 1.7:

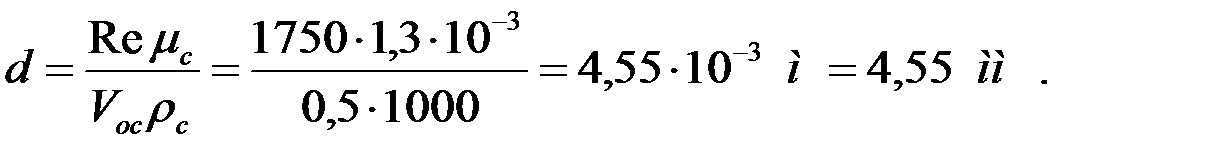
Задача 4. Найти скорость осаждения в воде при 20ºС частицы свинцового блеска угловатой формы с Плотность свинцового блеска 7560

Решение. Скорость осаждения частиц неправильной формы найдем из уравнения критерия Лященко (Ly), предварительно определив значение критерия Архимеда (Ar), формула 1.3:

где динамическая вязкость воды при температуре 20^оС, в приложении 2, табл. П.2.1;

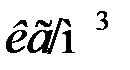,плотность воды при температуре 20^оС, в приложении 2, табл. П.2.1.

Скорость осаждения определяем по формуле 1.8:

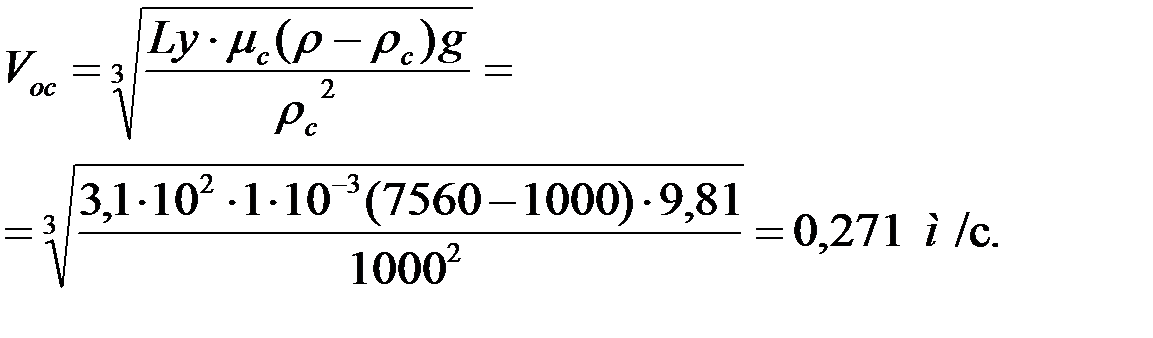
Задача 5. Определить размеры продолговатых частиц угля и плоских частиц сланца 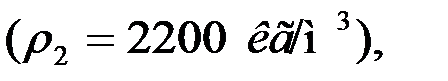, оседающих с одинаковой скоростью 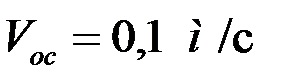в воде при температуре 20 ºС.

Решение. Размеры частиц следует рассчитать по формуле 1.11:

предварительно определив значение критерия Архимеда (Ar) по критерию Лященко (Ly) из графика (рис. 1) для частиц соответствующей формы.

Для частиц продолговатой формы:

где 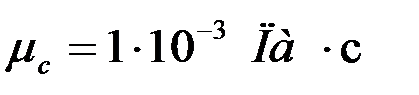динамическая вязкость воды при температуре воды (в приложении 2, табл. П.2.1);

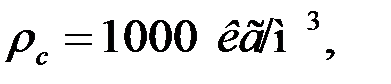плотность воды (в приложении 2, табл. П.2.1).

Для частиц пластинчатой формы:

Значению соответствует 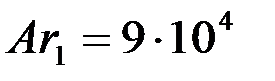для продолговатых частиц. Значению 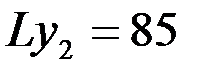соответствует для пластинчатой формы.

Эквивалентный диаметр частиц угля, формула 1.11:

Эквивалентный диаметр частиц сланца, формула 1.11:

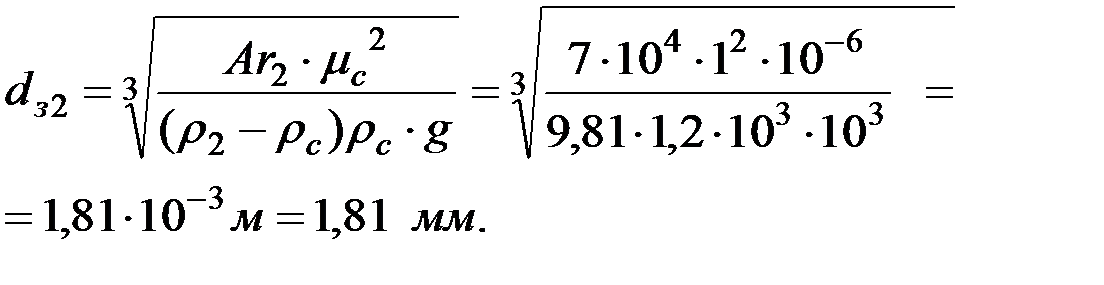
Задача 6. Какую высоту h надо дать слою газа между полками пылевой камеры (рис.3), чтобы осели частицы пыли диаметром 8 мкм при расходе печного газа J_о = 0,6 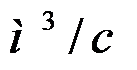(при нормальных условиях)? Длина камеры L = 4,1 м, ширина b = 2,8 м, общая высота H = 4,2 м. Средняя температура газа в камере t_cр = 427 ºС. Вязкость газа при этой температуре m = плотность пыли r_п = 4000 плотность газа r_г = 0,5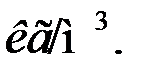

LL

b

H

h

V

V_ос

Рис. 2. Пылевая камера

L

Решение. Определяем расход газа при заданных условиях, т.е температуре 427 ºС:

Линейная скорость газа (пренебрегая толщиной полок):

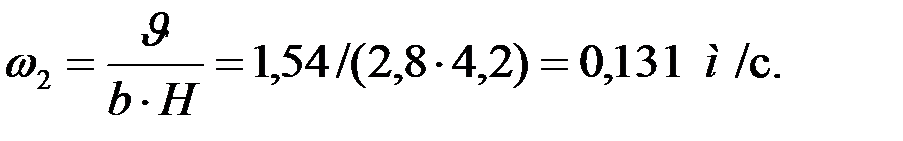
Время пребывания газа в камере:

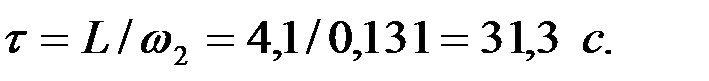
Теоретическую скорость осаждения шарообразных частиц (величиной пренебрегаем) определяется по формуле 1.2., предварительно предположив, что процесс ламинарный:

Действительную скорость осаждения находим, принимая условие 1.19:

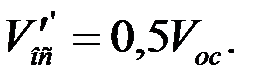= 0,5∙0,0041 = 0,002 м/c.

Находим расстояние между полками:

Определяем число Рейнольдса по преобразованной формуле 1.7., чтобы убедиться, что формула Стокса применима к нашим условиям задачи:

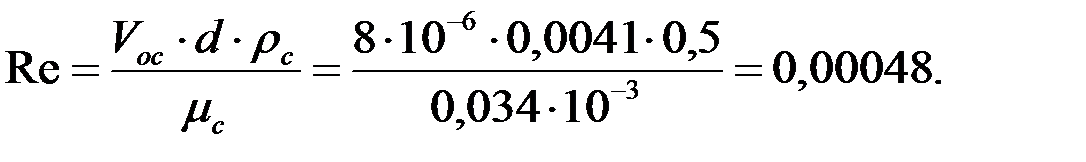
Так как Re = 0,00048 < 0,2, то применение формулы Стокса допустимо.

Задача 7. Определить размер наименьших частиц, осаждающихся в газоходе квадратного сечения длиной L = 16 м и высотой H = 2 м при линейной скорости газа w = 0,5 м/c. Вязкость газа m = плотность газа r_г = 0,8 плотность частиц r_ч = 4000

Решение. Газ проходит канал в сечении за время:

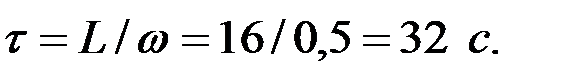
За это время успевают полностью осесть только те частицы, действительная скорость осаждения которых не меньше, чем:

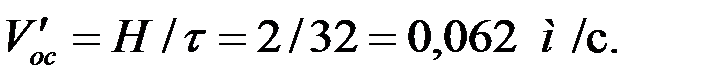
Определяем диаметр шарообразных частиц, теоретическая скорость осаждения которых вдвое больше действительной, т. е. равна 0,124 м/c.

Вычислим значение критерия Лященко (Ly) по формуле 1.5:

По графику (рис. 1) находим значение Re = 0,14, подставляем в формулу 1.7 и находим диаметр частицы:

Дата добавления: 2015-07-11