Осаждение в поле силы тяжести.

Для описания в критериальной форме процесса осаждения шарообразной частицы в неподвижной неограниченной среде могут быть применены критерии подобия: Архимеда (Ar), Лященко (Ly) и Рейнольдса (Re). Наиболее удобной формой критериальной зависимости является:

1. При так называемом ламинарном режиме осаждения, когда критерии имеют значения , можно использовать уравнение Стокса для определения скорости осаждения V_ос (м/с) шарообразной частицы:

(1.1)

Это же уравнение для осаждения частицы в газовой среде, так как можно величиной плотности газа (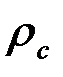) пренебречь, упрощается:

, (1.2)

где d – диаметр шарообразной частицы м;

– плотность частицы, ;

– плотность среды, ;

– динамический коэффициент вязкости среды, , т.е. , или

2. Для определения скорости осаждения по обобщенному методу, пригодному при любом режиме осаждения используем нижеприведенные формулы и график рис.1. Так, определение скорости осаждения шарообразной одиночной частицы в неподвижной неограниченной среде, осуществляют следующим образом. Определяем критерий Архимеда для жидкой среды:

(1.3)

где – критерий Галилея;

Re – критерий Рейнольдса;

Fr– критерий Фруда.

Для газообразной среды уравнение критерия Архимеда (Аr) изменится так:

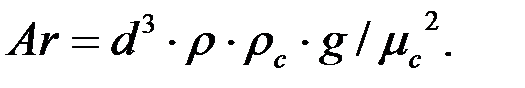(1.4)

По найденному значению критерия Архимеда (Ar) по графику рис. 1 определяют критерий Рейнольдса (Re) или критерий Лященко (Ly):

(1.5)

а для осаждения в газовой среде, критерий Лященко (Ly) изменится:

(1.6)

Далее вычисляем скорость осаждения:

(1.7)

или

(1.8)

Для частицы неправильной формы скорость осаждения определяют тем же путем используя критерий Лященко (Ly), но с подстановкой в критерий Архимеда (Аr) вместо d ® d_э. Эквивалентный диаметр частицы (d_э) неправильной формы вычисляют как диаметр условного шара, объем которого u равен объему тела неправильной формы:

(1.9)

где М – масса частицы, кг.

3. Диаметр осаждающей шарообразной частицы при известной скорости осаждения находят обратным путем, т.е. вычисляют сначала критерий Лященко (Ly):

(1.10)

и по найденному значению критерия Лященко (Ly), определяем критерий Архимеда (Ar), используя график (рис. 1). Преобразуя формулу (1.3), вычисляем диаметр шарообразной частицы.

4. Эквивалентный диаметр частицы твердого тела неправильной формы при известной скорости осаждения определяем таким же путем. Сначала определяем критерий Лященко (Ly) по формуле (1.10), затем находим значение критерия Архимеда (Ar) из графика (рис. 1) для частицы соответствующей формы и вычисляем ее эквивалентный диаметр:

(1.11)

5. В свою очередь, если уже подсчитана скорость осаждения для частиц шарообразной формы, но на самом деле, её форма отлична от шарообразной, то скорость осаждения можем найти используя коэффициент f:

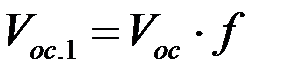(1.12)

где V_ос.1 – скорость осаждения частиц с формой отличной от шарообразной;

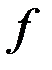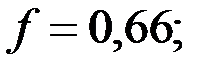– коэффициент, учитывающий форму частиц (для частиц округлых для угловатых для продолговатых 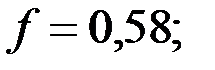для пластинчатых ).

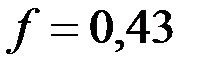Рис. 1. Графикзависимостей критериев Re и Ly от критерия Ar для осаждения одиночной частицы в неподвижной среде:

1 и 6 – шарообразные частицы; 2 – округленные;

3 – угловатые; 4 – продолговатые; 5 – пластинчатые.

6. Если рассматривается процесс осаждения не одной частицы, а нескольких, то скорость осаждения уже зависит концентрации этих частиц в жидкости или газе. Такую скорость называют скоростью стесненного осаждения.

Определим аналитическим способ скорость стесненного осаждения:

(1.13.)

где V_ос.2. – скорость осаждения в стесненных условиях, с учетом отклонения форм частиц от шарообразных;

l – коэффициент, учитывающий стесненные условия осаждения, определяется по формуле Андерса:

(1.14)

где С_v – концентрация сухих веществ в суспензии.

7. Площадь осаждения () пылеосадительной камеры или отстойника для суспензий (взвесей) определяется по формуле:

(1.15)

или:

(1.16)

где u – объемный расход газа (жидкости), проходящего через аппарат параллельно поверхности осаждения, ;

– средняя действительная скорость осаждения частиц, ;

1,3 – коэффициент, учитывающий возможную перегрузку отстойника;

– плотность осветлённой жидкости, кг/м³;

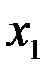и – содержание твердой фазы в суспензии до и после отстаивания, мас. %;

– количество суспензии, полученной при отстаивании, кг/с.

Количество осветлённой жидкости u_о, (м³/с) определяем по формуле 1.17:

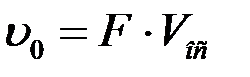(1.17)

Продолжительность осаждения 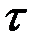, (с), частицы в слое высотой h, (м), определяется по формуле 1.18:

(1.18)

При ориентировочных расчетах, учитывая приближенно отличие реальных условий осаждения от теоретических (стесненность осаждения, форма частиц, движение среды), среднюю действительную скорость осаждения V^/_ос, часто принимают равной половине теоретической расчетной скорости осаждения V_ос одиночной шарообразной частицы:

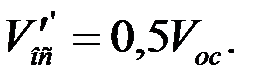(1.19)

Дата добавления: 2015-07-11