
Читайте также:
|
36. Распределение температуры в любой точке бесконечной пластины для любого момента времени:
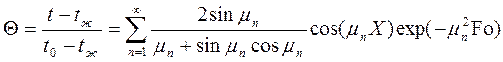 ,
,
здесь  – безразмерная координата,
– безразмерная координата,  – число Фурье;
– число Фурье; 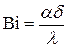 – число Био; m n – корни характеристического уравнения
– число Био; m n – корни характеристического уравнения 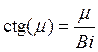 .
.
37. Распределение температуры в пластине, если число Фурье превышает 0,3:
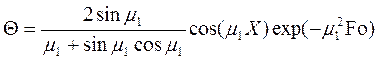 .
.
38. Средняя безразмерная избыточная температура:
 .
.
39. Количество теплоты отданное (полученное) пластиной в процессе охлаждения (нагревания):
 , где
, где
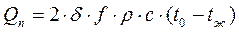 ,
,
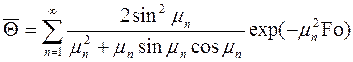 .
.
ЗАДАЧИ
55. Резиновая пластина толщиной 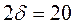 мм, нагретая до температуры
мм, нагретая до температуры 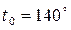 С, помещена в воздушную среду с температурой
С, помещена в воздушную среду с температурой 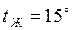 С. Определить температуры в середине и на поверхности пластины через
С. Определить температуры в середине и на поверхности пластины через 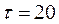 мин после начала охлаждения, а также температуру на расстоянии
мин после начала охлаждения, а также температуру на расстоянии 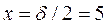 мм от середины пластины. Коэффициент теплопроводности резины
мм от середины пластины. Коэффициент теплопроводности резины 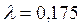 Вт/(м оС). Коэффициент температуропроводности резины
Вт/(м оС). Коэффициент температуропроводности резины  м2/с. Коэффициент теплоотдачи от поверхности пластины к окружающему воздуху
м2/с. Коэффициент теплоотдачи от поверхности пластины к окружающему воздуху  Вт/(м2
Вт/(м2 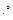 С). Ответ:
С). Ответ: 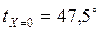 С;
С; 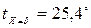 С.
С.
Решение:
Температуры в середине и на поверхности безграничной пластины при охлаждении (нагревании) в среде с постоянной температурой можно определить с помощью графиков (см. рис. 4 и 5). В рассматриваемом случае 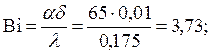
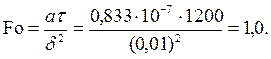 При этих значениях чисел Био и Фурье по графику на рис. 4 находим Q x=0 = 0,26 и по графику на рис. 5 Q x=d = 0,083. Из определения безразмерной избыточной температуры находим температуры центра и поверхности пластины:
При этих значениях чисел Био и Фурье по графику на рис. 4 находим Q x=0 = 0,26 и по графику на рис. 5 Q x=d = 0,083. Из определения безразмерной избыточной температуры находим температуры центра и поверхности пластины: 
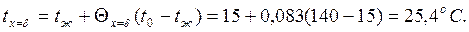
56. Для условий предыдущей задачи определить безразмерные температуры в середине и на поверхности пластины расчетным путем. Результаты сравнить с данными, полученными из графиков в предыдущей задаче. Ответ: 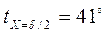 С;
С;  ;
;  .
.
Решение:
Безразмерная температура неограниченной пластины при охлаждении в среде с постоянной температурой для случая Fo=1>0,3 выражается уравнением 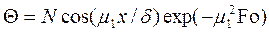 . Значения величин N, P, m 1 и m 21 – приведены в таблице 8. В рассматриваемом случае для Bi=3,73 находим: N = 1,224; P = 0,390; m 1 = 1,248; m 21 = 1,56. Следовательно, при Fo=1:
. Значения величин N, P, m 1 и m 21 – приведены в таблице 8. В рассматриваемом случае для Bi=3,73 находим: N = 1,224; P = 0,390; m 1 = 1,248; m 21 = 1,56. Следовательно, при Fo=1: 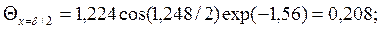
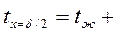

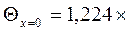
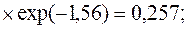
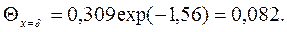
57. Определите промежуток времени, по истечении которого лист стали, прогретый до температуры 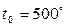 С, будучи помещен в воздушную среду, температура которой
С, будучи помещен в воздушную среду, температура которой  С, примет температуру, отличающуюся не более чем на 1 % от температуры окружающей среды. Толщина листа стали
С, примет температуру, отличающуюся не более чем на 1 % от температуры окружающей среды. Толщина листа стали 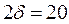 мм. Коэффициент теплопроводности стали
мм. Коэффициент теплопроводности стали 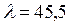 Вт/(м оС); теплоемкость стали
Вт/(м оС); теплоемкость стали 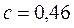 кДж/(кг оС), плотность стали
кДж/(кг оС), плотность стали 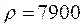 кг/м3. Коэффициент теплоотдачи от поверхности листа к окружающему воздуху
кг/м3. Коэффициент теплоотдачи от поверхности листа к окружающему воздуху 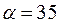 Вт/(м2 оС). Ответ: 2 ч 15 мин.
Вт/(м2 оС). Ответ: 2 ч 15 мин.
58. Определите время  необходимое для нагрева листа стали толщиной
необходимое для нагрева листа стали толщиной  мм, который имел начальную температуру
мм, который имел начальную температуру  С, а затем был помещен в печь с температурой
С, а затем был помещен в печь с температурой 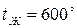 С. Нагрев считать законченным, когда температура листа достигнет значения
С. Нагрев считать законченным, когда температура листа достигнет значения 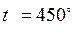 С. Коэффициент теплопроводности, теплоемкость и плотность стали равны соответственно
С. Коэффициент теплопроводности, теплоемкость и плотность стали равны соответственно  Вт/(м оС);
Вт/(м оС);  кДж/(кг оС);
кДж/(кг оС);  кг/м3, а коэффициент теплоотдачи к поверхности листа
кг/м3, а коэффициент теплоотдачи к поверхности листа 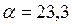 Вт/(м2 оС). Ответ: t = 45 мин.
Вт/(м2 оС). Ответ: t = 45 мин.
59. Кирпичная стена толщиной 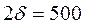 мм обеими поверхностями соприкасается со средой, имеющей постоянную температуру 18°С. Коэффициенты теплопроводности, температуропроводности и плотность материала соответственно равны:
мм обеими поверхностями соприкасается со средой, имеющей постоянную температуру 18°С. Коэффициенты теплопроводности, температуропроводности и плотность материала соответственно равны: 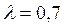 Вт/(м оС);
Вт/(м оС); 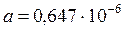 м2/с;
м2/с; 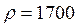 кг/м3. Как изменится температура на поверхности и в середине кладки в течение 1 ч, если температура среды внезапно понизилась до 8°С? Коэффициент теплоотдачи с поверхности кладки остается постоянным и равным 7 Вт/(м2 оС). Ответ: Температура поверхности кладки tп = 14,3оС, середины кладки – tц = 18оС.
кг/м3. Как изменится температура на поверхности и в середине кладки в течение 1 ч, если температура среды внезапно понизилась до 8°С? Коэффициент теплоотдачи с поверхности кладки остается постоянным и равным 7 Вт/(м2 оС). Ответ: Температура поверхности кладки tп = 14,3оС, середины кладки – tц = 18оС.
60. Стальная пластина толщиной 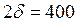 мм нагревается в печи, имеющей постоянную температуру
мм нагревается в печи, имеющей постоянную температуру 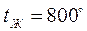 С. Температура пластины в момент помещения ее в печь была всюду одинаковой и равной
С. Температура пластины в момент помещения ее в печь была всюду одинаковой и равной 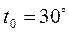 С. Коэффициент теплоотдачи к поверхности пластины в процессе нагрева оставался постоянным и равным
С. Коэффициент теплоотдачи к поверхности пластины в процессе нагрева оставался постоянным и равным  Вт/(м2 оС). Два других размера пластины велики по сравнению с толщиной и температурное поле пластины можно рассматривать как одномерное. Определить количество теплоты, которое будет подведено к 1 м2 пластины в течение 2 ч после начала нагрева. Коэффициенты теплопроводности, температуропроводности и плотность стали соответственно равны:
Вт/(м2 оС). Два других размера пластины велики по сравнению с толщиной и температурное поле пластины можно рассматривать как одномерное. Определить количество теплоты, которое будет подведено к 1 м2 пластины в течение 2 ч после начала нагрева. Коэффициенты теплопроводности, температуропроводности и плотность стали соответственно равны: 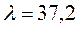 Вт/(м оС);
Вт/(м оС);  м2/с;
м2/с; 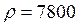 кг/м3. Ответ: Qср = 0,098; Q = 1470 МДж/м2.
кг/м3. Ответ: Qср = 0,098; Q = 1470 МДж/м2.
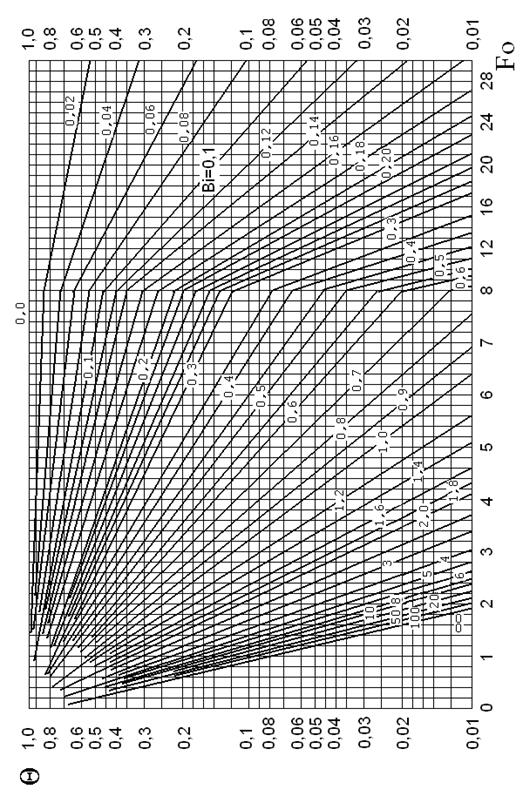
Рис. 4 – Номограмма для середины тонкой пластины

Рис. 5 – Номограмма для поверхности тонкой пластины
Дата добавления: 2015-07-11; просмотров: 959 | Нарушение авторских прав