Плоская стенка

1. Дифференциальное уравнение теплопроводности:

.

2. Плотность теплового потока в случае теплопроводности:

3. Распределение температуры в стенке:

4. Тепловой поток через поверхность F твердой стенки:

5. Плотность теплового потока для многослойной плоской стенки, состоящей из n однородных слоев:

,

где – термическое сопротивление теплопроводности i -го слоя стенки.

6.Температура в плоскости соприкосновения слоев:

7. Коэффициент теплопередачи от одной жидкой среды к другой через разделяющую их твердую стенку:

,

где R – полное термическое сопротивление теплопередачи многослойной плоской стенки.

8. Температуры поверхностей стенки при теплопередаче:

и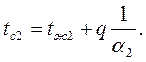

9. Распределение температуры внутри пластины при наличии внутренних источников тепла, в случае симметричных условий охлаждения:

.

10. Распределение температуры внутри пластины и температуры ее стенок при наличии внутренних источников тепла, в случае несимметричных условий охлаждения:

,

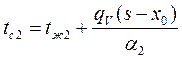и , где

.

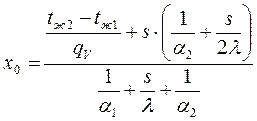ЗАДАЧИ

1. Решите дифференциальное уравнение теплопроводности в общем виде: 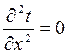со следующими граничными условиями: t (0) = t _c1, t (d) = t _c2. Ответ:

Решение:

Первое интегрирование дифференциального уравнения дает . После второго интегрирования получим . Подставляем граничные условия: при х = 0, t = t _c1, С ₂ = t _c1; при х = d, t = t _c2, ; тогда .

2. Решите одномерную задачу теплопроводности для пластины с внутренними источниками тепла: . Граничные условия: при .

Указания к решению. Поскольку граничные условия для обеих сторон пластины одинаковые, температурное поле внутри пластины должно быть симметричным относительно плоскости х = 0. Тепло с одинаковой интенсивностью отводится через левую и правую поверхности тела. Одинаково и тепловыделение в обеих половинах пластины. Решить задачу для правой половины пластины.

Ответ: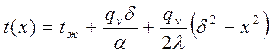

3. Решите уравнение теплопроводности в цилиндрических координатах: со следующими граничными условиями: t(r ₁) = t _c1, t(r ₂) = t _c2. Ответ:

Указания к решению. Решите задачу, воспользовавшись заменой переменных .

4. Решите задачу теплопроводности с внутренними источниками тепла в цилиндрических координатах: . Граничные условия: а) условие симметрии в центре стержня: r = 0: ; б) теплоотдача с поверхности: r = r ₀: .

Ответ:

5. Решите нестационарную одномерную задачу теплопроводности без внутренних источников тепла в декартовых координатах: . Начальные условия: при t = 0 . Граничные условия: при x = 0 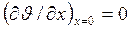; при х = d . Решиеь дифференциальное уравнением методом Фурье.

Ответ:

6. Вычислить плотность теплового потока через плоскую однородную стенку, толщина которой значительно меньше ширины и высоты, если стенка выполнена: а) из стали [ l = 50 Вт/(м ^оС)]; б) из бетона [ l = 1,1 Вт/(м ^оС)]; в) из диатомитового кирпича [ l = 0,11 Вт/(м ^оС)]. Во всех трех случаях толщина стенки d = 50 мм. Температуры на поверхностях стенки поддерживаются постоянными: t_{с 1} = 100^оС и t_{с 2} = 90^оС. Ответ: а) q = 10000 Вт/м²; б) q = 220 Вт/м²; в) q = 22 Вт/м².

7. Плотность теплового потока через плоскую стенку толщиной d = 100 мм q = 70 Вт/м². Определить разность температур на поверхностях стенки и численные значения градиента температуры в стенке, если она выполнена а) из латуни [ l = 70 Вт/(м ^оС)]; б) из красного кирпича [ l = 0,7 Вт/(м ^оС)]; в) из пробки [ l = 0,07 Вт/(м ^оС)]. Ответ: а) С и |grad t| = 1^оС/м; б) С и |grad t| = 100^оС/м; в) С и |grad t| = 1000^оС/м.

8. Определить потерю теплоты Q (Вт) через стенку из красного кирпича длиной l = 5 м, высотой h = 4 м и толщиной d = 500 мм, если температуры на поверхностях стенки поддерживаются t_{с 1} = 110^оС и t_{с 2} = 40^оС. Коэффициент теплопроводности красного кирпича l = 0,7 Вт/(м ^оС). Ответ: Q = 1960 Вт.

9. Определить коэффициент теплопроводности материала стенки, если при толщине ее мм и разности температур на поверхностях ^оС плотность теплового потока q = 175 Вт/м². Ответ: l = 0,35 Вт/(м ^oС).

10. Плоская стенка выполнена из шамотного кирпича толщиной d = 250 мм. Температура ее поверхностей t_{c 1} = 1350^оС и t_{c 2} = 50^оС. Коэффициент теплопроводности шамотного кирпича является функцией от температуры l = 0,838^.(1 + 0,00007 t). Вычислить и изобразить в масштабе распределение температуры в стенке. Ответ:

x, мм
t, ^oC

Решение:

В случае линейной зависимости коэффициента теплопроводности от температуры плотность теплового потока, , где средний коэффициент теплопроводности, . В рассматриваемом случае: 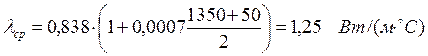и . Температура на любом расстоянии x от поверхности стенки определяется по формуле . Подставив известные и найденные величины, получим . Подставим в полученное уравнение значения х, выраженные в метрах, найдем соответствующие значения температуры стенки.

11. Температуры на поверхностях шамотной стенки, толщина которой мм, равны ^оС и ^оС. Коэффициент теплопроводности шамота изменяется в зависимости от температуры по уравнению . Показать, что плотность теплового потока q в случае линейной зависимости коэффициента теплопроводности от температуры может быть вычислена по формуле для постоянного коэффициента теплопроводности, взятого при средней температуре стенки. Найти ошибку в определении температуры в точках x =57,5; 110 и 157,5 мм, если вычисления производятся по значению коэффициента теплопроводности, среднему для заданного интервала температур, и построить график распределения температуры в стенке. Ответ: q=4650 Вт/м².

12. Плоская стенка бака площадью F =5 м² покрыта двухслойной тепловой изоляцией. Стенка бака стальная, толщиной d ₁ = 8 мм, с коэффициентом теплопроводности l ₁= 46,5 Вт/(м ^оС). Первый слой изоляции выполнен из новоасбозурита толщиной d ₂ = 50 мм, коэффициент теплопроводности которого определяется уравнением l ₂= 0,144 + 0,00014 t. Второй слой изоляции толщиной d ₃ = 10 мм представляет собой известковую штукатурку, коэффициент теплопроводности которой l ₃= 0,698 Вт/(м ^оС). Температуры внутренней поверхности стенки бака t_{c 1} = 250^оС и внешней поверхности изоляции t_{c 4} = 50^оС. Вычислить количество теплоты, передаваемой через стенку, температуры на границах слоев изоляции и построить график распределения температуры. Ответ: Q = 3170 Вт, t_c2 = 249,9^оC и t_c3 = 59^оC.

13. Обмуровка печи состоит из слоев шамотного и красного кирпича, между которыми расположена засыпка из диатомита. Толщина шамотного слоя d ₁ = 120 мм, диатомитовой засыпки d ₂ = 50 мм и красного кирпича d ₃ = 250 мм. Коэффициенты теплопроводности материалов соответственно равны l ₁= 0,93; l ₂= 0,13 и l ₃ = 0,7 Вт/(м ^оС). Какой толщины следует сделать слой из красного кирпича, если отказаться от применения засыпки из диатомита, чтобы тепловой поток через обмуровку остался неизменным? Ответ: толщина слоя красного кирпича должна быть равна 500 мм.

14. Стенка неэкранированной топочной камеры парового котла выполнена из слоя пеношамота толщиной d ₁ = 125 мм и слоя красного кирпича толщиной d ₂ = 500 мм. Слои плотно прилегают друг к другу. Температура на внутренней поверхности топочной камеры t_{c 1} = 1100^оС, а на наружной t_c3 = 50^оС. Коэффициент теплопроводности пеношамота l ₁= 0,28 + 0,00023 t, красного кирпича l ₂= 0,7 Вт/(м ^оС). Вычислить тепловые потери через 1 м²стенки топочной камеры и температуру в плоскости соприкосновения слоев. Ответ: q=1090 Вт/м², t_{c 2} = 828^oC.

15. Толщину слоя красного кирпича в стенке топочной камеры, рассмотренной в предыдущей задаче, решено уменьшить в 2 раза, а между слоями поместить слой засыпки из диатомитовой крошки, коэффициент теплопроводности которой . Какую нужно сделать толщину диатомитовой засыпки, чтобы при тех же температурах на внешних поверхностях стенки, что и в предыдущей задаче, потери теплоты оставались неизменными? Ответ: d = 94мм.

16. Стены сушильной камеры выполнены из слоя красного кирпича толщиной мм и слоя строительного войлока. Температура на внешней поверхности кирпичного слоя 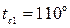С и на поверхности войлочного слоя С. Коэффициенты теплопроводности материалов равны соответственно и Вт/(м ^оС). Вычислить температуру в плоскости соприкосновения слоев и толщину войлочного слоя при условии, что тепловые потери через 1 м² стенки камеры не превышают q =110 Вт/м². Ответ: t_{c 2} = 828^oC, d ₂ = 50 мм.

17. Определить тепловой поток через 1 м² кирпичной стены помещения толщиной в два кирпича (d = 510 мм) с коэффициентом теплопроводности l = 0,8 Вт/(м ^оС). Температура воздуха внутри помещения t_{ж 1} = 18^оС; коэффициент теплоотдачи к внутренней поверхности стенки a₁ =7,5 Вт/(м^{2 о}С); температура наружного воздуха t_{ж 2} = –30^оС; коэффициент теплоотдачи от наружной поверхности стены, обдуваемой ветром, a₂ =20 Вт/(м^{2 о}С). Вычислить также температуры на поверхностях стены и . Ответ: q=58,6 Вт/м².

18. Решить предыдущую задачу, если стена покрыта снаружи слоем тепловой изоляции толщиной 50 мм с коэффициентом теплопроводности λ=0,08 Вт/(м ^оС). Сравнить потери теплоты через изолированную и неизолированную стенки. Ответ: q=33,2 Вт/м², и . Потери теплоты через неизолированную стенку на 76,5% больше, чем через изолированную.

19. Обмуровка печи выполнена из слоя шамотного кирпича с коэффициентом теплопроводности Вт/(м ^оС); толщина обмуровки мм. Определить потери теплоты с одного квадратного метра поверхности q (Вт/м²) и температуры на внешних поверхностях стены, если температура газов в печи и воздуха в помещении , коэффициент теплоотдачи от газов к стенке Вт/(м^{2 о}С) и от обмуровки к окружающему воздуху Вт/(м^{2 о}С). Ответ: q=3530 Вт/м².

Указания к решению. При заданной зависимости коэффициента теплопроводности шамотного кирпича от температуры потери теплоты можно вычислить из уравнения

или методом последовательных приближений. Приведем алгоритм метода последовательных приближений.

1. Примем температуры стенки, равными соответствующим температурам среды.

2. Зададим среднюю температуру стенки.

3. Определим по средней температуре стенки среднее значение коэффициента теплопроводности.

4. По среднему значению коэффициента теплопроводности рассчитаем коэффициент теплопередачи и плотность теплового потока.

5. По полученному значению плотности теплового потока находим температуры на поверхностях стенки.

6. Повторяем вычисления, начиная со второго пункта, до тех пор, пока значение коэффициента теплопроводности практически совпадет с принятым ранее значением.

20. В камере сгорания парового котла с жидким золоудалением температура газов должна поддерживаться равной , температура воздуха в котельной . Стены топочной камеры выполнены из слоя огнеупора толщиной мм с коэффициентом теплопроводности Вт/(м ^оС) и слоя диатомитового кирпича с коэффициентом теплопроводности Вт/(м ^оС). Коэффициент теплоотдачи от газов к обмуровке Вт/(м^{2 о}С) и от внешней поверхности топочной камеры к окружающему воздуху Вт/(м^{2 о}С). Какой должна быть толщина диатомитового слоя, чтобы потери в окружающую среду не превышали 750 Вт/м². Ответ: мм.

21. Длительно допустимая сила тока для стальных шин прямоугольного сечения мм, установленных на ребро, не должна превышать 300 А. Максимальная температура шины при температуре окружающего воздуха должна быть не выше . Вычислить температуру на поверхности шины и определить, каким должен быть коэффициент теплоотдачи с ее поверхности, чтобы температура шины не превышала максимально допустимого значения . Коэффициент теплопроводности стали Вт/(м ^оС). Удельное электрическое сопротивление стали Ом мм²/м. Ответ: ; Вт/(м^{2 о}С).

22. По электрическому нагревателю, выполненному из константановой ленты сечением мм и длиной 1 м, протекает электрический ток 20 А. Падение напряжения на концах нагревателя 200 В. Определить температуры поверхности ленты и середины по ее толщине, если коэффициент теплоотдачи на поверхности нагревателя 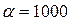Вт/(м^{2 о}С), температура среды 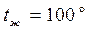С и коэффициент теплопроводности константана Вт/(м ^оС). Ответ: t_с=433^oC, t₀=437^oC.

23. Пластина с равномерно распределенными внутренними источниками теплоты симметрично охлаждается с обеих поверхностей. Температура охлаждающей жидкости равна . В этих условиях температуры на поверхностях , а максимальная температура в середине пластины равна . Определить, чему будут равны температуры и на поверхностях пластины, если прекратится отвод теплоты через одну из поверхностей (). Ответ: ; .

24. Пластина с равномерно распределенными внутренними источниками теплоты 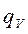(Вт/м³) обтекается с двух сторон жидкостью. Толщина пластины s (м), коэффициент теплопроводности ее материала l, измеряется в Вт/(м ^оС). Температура жидкости со стороны одной из поверхностей равна (^оС) и коэффициент теплоотдачи от этой поверхности к жидкости равен в Вт/(м^{2 о}С). Определить значение температуры жидкости со стороны другой поверхности , при которой тепловой поток через эту поверхность будет равен нулю (). Ответ: .

25. Пластина с равномерно распределенными внутренними источниками теплоты , обтекается с обеих сторон жидкостью. Коэффициенты теплоотдачи от поверхностей пластины к жидкости и температуры жидкостей соответственно равны a₁ и a₂, и . Толщина пластины s, коэффициент теплопроводности ее материала l. а) Определить соотношение между разностью температур и коэффициентами теплоотдачи a₁ и a₂ для случая, когда максимум температуры находится в середине пластины: . б) Определить, чему равна разность при , если . в) Найти выражение для при равенстве температур и . Ответ: а) ; б) ; в) .

26. В пластине толщиной s = 5мм действуют равномерно распределенные внутренние источники теплоты Вт/м³. Коэффициент теплопроводности материала пластины Вт/(м ^оС). Коэффициенты теплоотдачи от поверхностей пластины к обтекающей их жидкости Вт/(м^{2 о}С) и Вт/(м^{2 о}С), а температуры жидкости соответственно равны и . Определить координату и значение максимальной температуры в пластине х₀ и t₀, а также температуры на поверхностях пластины t_с1 и t_с2. Ответ: ; ; ; .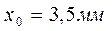

Решение:

Относительная координата максимальной температуры в пластине при , , несимметричном температурном поле и граничных условиях третьего рода , где x₀ отсчитывается от поверхности, обтекаемой жидкостью с температурой 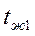. В рассматриваемом случае , мм.

Температуры на поверхностях пластины:

;

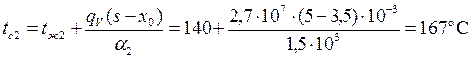
Максимальная температура

.

Дата добавления: 2015-07-11