Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Математические свойства дисперсии.

⇐ ПредыдущаяСтр 10 из 24Следующая ⇒


Читайте также:
  1. II. Собственно свойства пульса.
  2. III. Психические свойства, влияющие на безопасность.
  3. V2: Механические свойства материалов
  4. Алюминий: физические свойства, получение, применение, история
  5. Аметист камень - свойства.
  6. Ассортимент, потребительские свойства, экспертиза качества молока и молочных продуктов
  7. Ассортимент, потребительские свойства, экспертиза качества рыбы и рыбных продуктов

1. Дисперсия, рассчитанная по отношению к средней величине, является минимальной.

2. Дисперсия постоянной величины равна 0.

3. Если все значения признака (варианты) увеличить (уменьшить) на какое-то постоянное число А, то дисперсия новой совокупности не изменится.

4. Если все значения признака (варианты) увеличить (умножить) в К раз, где К – постоянное число, то дисперсия новой совокупности увеличится (уменьшится) в К2 раз.

5. Если вычислена дисперсия по отношению к числу В, отличному от средней величины, то дисперсию исходной совокупности можно рассчитать по формуле: .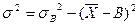

6. Дисперсию исходной совокупности можно рассчитать как разность между средней квадратов признака и квадратом средней величины.

 

Дата добавления: 2015-07-11; просмотров: 67 | Нарушение авторских прав

⇐ Предыдущая3456789101112131415161718Следующая ⇒



mybiblioteka.su - 2015-2024 год. (0.01 сек.)