|
Читайте также: |
Если исходная совокупность разделена на группы по какому-то существенному признаку, то вычисляют следующие виды дисперсий:
1) Общую дисперсию исходной совокупности по формуле: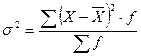 
, где 
- общая средняя величина исходной совокупности; f – частоты исходной совокупности. Общая дисперсия характеризует отклонение индивидуальных значений признака от общей средней величины исходной совокупности.
2) Внутригрупповые дисперсии по формуле: 
, где j - номер группы; 
- средняя величина в каждой j-ой группе; 
- частоты j-ой группы. Внутригрупповые дисперсии характеризуют отклонение индивидуального значения признака в каждой группе от групповой средней величины. Из всех внутригрупповых дисперсий вычисляют среднюю по формуле: 
, где 
- численность единиц в каждой j-ой группе.
3) Межгрупповую дисперсию по формуле: 
. Межгрупповая дисперсия характеризует отклонение групповых средних величин от общей средней величины исходной совокупности. Правило сложения дисперсий заключается в том. что общая дисперсия исходной совокупности должна быть равна сумме межгрупповой и средней из внутригрупповых дисперсий: 
. Результат отношения межгрупповой к общей дисперсии исходной совокупности называется эмпирическим коэффициентом детерминации. Он показывает долю вариации изучаемого признака, обусловленную вариацией группировочного признака.
Дата добавления: 2015-07-11; просмотров: 67 | Нарушение авторских прав