|
Читайте также: |
Медиана – это значение признака при котором исходная совокупность делится на 2 равные части, при этом первая половина совокупности имеет значение признака меньше, чем медиана, а вторая имеет значения признака больше, чем медиана.
Квартиль делит исходную совокупность на 4 равные части. На практике вычисляют первый (нижний) квартиль, который делит исходную совокупность в соотношении ¼: ¾ и третий (верхний) квартиль, который делит исходную совокупность в соотношении ¾: ¼.
Дециль делит исходную совокупность на 10 равных частей. Например: второй D делит исходную совокупность в соотношении 2/10: 8/10; девятый D делит исходную совокупность в соотношении 9/10: 1/10.
В дискретном вариационном ряду для определения Ме, квартилей и децилей необходимо:
1) Вычислить накопленные частоты.
2) Определить порядковый номер единицы, которая делит исходную совокупность в нужном нам соотношении. Например: для Ме: 
; для первого Q: 
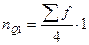; для девятого D: 
.
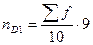3) По накопленным частотам найти значение признака, которое имеет нужная нам единица совокупности. Пример (про семьи):
| Число детей | Количество семей | S |
| Х | ƒ | |
| Итого |
По накопленным частотам определяем, что 10-ой единице совокупности (10-ой семье) соответствует значение признака равное 1, значит Ме равна 1 ребенку. Половина семей имеют 1 ребенка и вообще не имеют детей, а вторая половина имеют 1 ребенка и больше. 
; 
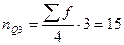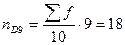Таким образом мы вычислили, что ¾ семей (75%) имеют 2-ух детей и меньше, а 25% семей имеют более 2-ух детей; 90% семей имеют 3-ех детей и меньше, а 10% более 3-ех детей.
В интервальном вариационном ряду для определения медианы, квартилей и децилей необходимо:
1) Вычислить накопленные частоты.
2) Найти порядковый номер единицы, которая делит исходную совокупность в нужном нам соотношении.
3) По накопленным частотам найти интервал, содержащий нужную нам единицу совокупности.
4) Медиану, квартили и децили вычисляют по формулам: 
, где 
- нижняя граница медианного интервала (интервала, содержащего единицу, которая делит всю совокупность на 2 равные части); 
- величина медианного интервала;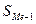 
- накопленная частота интервала, предшествующего медианному; 
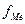- частота медианного интервала. Пример:
| Возраст депутата (полных лет) (X) | Численность депутатов (кол-во человек) (ƒ) | S |
| 20-29 | ||
| 30-39 | ||
| 40-49 | ||
| 50-59 | ||
| 60-69 | ||
| Итог: |
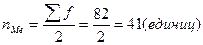По накопленным частотам определяем, что 41-ая единица совокупности содержится в интервале 40-49 лет. Этот интервал является медианным.
Половина депутатов фракции «Единство» моложе 47,7 лет, 2-ая половина старше 47,7 лет.
В интервальном вариационном ряду медиану можно вычислить графически по кумуляте:
Квартиль вычисляют по формуле: 
; 
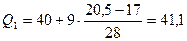
Дециль вычисляют по формуле: 
.
В интервальном вариационном ряду квартиль и дециль можно вычислить графически по кумуляте:
Показатели вариации.
Изменение величины признака от одной единицы совокупности к другой в статистике называют вариацией признака. Кроме средних величин для анализа исходной совокупности вычисляют абсолютные и относительные показатели вариации. К абсолютным показателям относятся:
1) Размах вариации (R) определяется, как разность между максимальным и минимальным значением признака в исходной совокупности R=Xmax-Xmin.
2) Среднее квартильное отклонение. Определяется как половина разности 3-его и 1-ого квартиля: 
.
3) Среднее линейное отклонение (d). Определяется, как средняя арифметическая величина из абсолютных отклонений индивидуальных значений признака от их средней величины. Применяют 2 формулы для не сгруппированных данных и сгруппированных.
Для не сгруппированных: 
; для сгруппированных: 
.
4) Дисперсия (
). Определяется, как средняя арифметическая величина из квадратов отклонений индивидуальных значений признака от из средней величины.
Для не сгруппированных: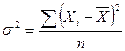 
; для сгруппированных: 
.
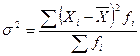5) Среднее квадратическое отклонение представляет собой квадратный корень из дисперсии.
Для не сгруппированных: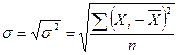 
; для сгруппированных: 
.
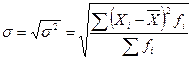Среднее квадратическое отклонение показывает на сколько в среднем отличаются индивидуальные значения признака (варианты) в исходной совокупности от средней величины. Показатель среднего квадратического отклонения применяется при оценке возможного риска в финансово-экономических расчетах.
Дата добавления: 2015-07-11; просмотров: 69 | Нарушение авторских прав