Средние величины. Средняя величина является одной из важнейших обобщающих характеристик статистики

Средняя величина является одной из важнейших обобщающих характеристик статистики. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами, и находят выражение общие и закономерные черты, свойственные всей совокупности в целом. Индивидуальные значения признака (варианты), из которых вычисляется средняя величина, должны быть одного и того же вида, т. е. должны характеризовать однородные явления и иметь одинаковые единицы измерения.

В каждом конкретном случае средняя величина имеет определенное, социально-экономическое содержание, обусловленное природой изучаемого объекта. Например: Средняя зарплата первого сотрудника определяется путем деления фонда оплаты труда на численность сотрудников. Средний размер вклада в банке определяется путем деления суммы все вкладов.

В статистике вычисляют степенные и структурные средние величины. Общая формула степенных средних величин имеет следующий вид: . В этой формуле X_i – индивидуальное значение признаков (варианты); ƒ_i – соответствующие частоты (частости); m – показатель степени. Различают следующие виды степенных средних величин: 1) При m = 1 → средняя арифметическая величина. 2) При m = -1 → средняя гармоническая величина. 3) При m = 0 → средняя геометрическая величина. 4) При m = 2 → средняя квадратичная величина. 5) При m = 3 → средняя кубическая величина.

Выбор формулы для расчета средней величины зависит от имеющейся исходной информации.

Средняя арифметическая величина.

Вычисляют простую и взвешенную среднюю арифметическую величину. Формула простой имеет следующий вид: 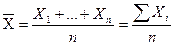. Эта формула применяется в тех случаях, когда исходные данные не сгруппированы (не образованы в группы пол какому-то признаку) и каждой единице совокупности соответствует определенное значение признака, либо, когда все частоты (частости) равны между собой. Формула средней арифметической взвешенной величины имеет следующий вид: 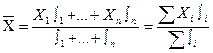. Эта формула применяется в тех случаях, когда исходные данные сгруппированы, и каждой группе единиц совокупности соответствует определенное значение признака (вариант). Пример: Приводится группировка депутатов фракции «Единство» Государственной Думы по возрасту на 16 января 2002 года:

Возраст депутата (полных лет) (X)	Численность депутатов (кол-во человек) (ƒ)	Середины интервалов (X)	X* ƒ
20-29		24,5	24,5
30-39		34,5
40-49		44,5
50-59		54,5
60-69		64,5	451,5
Итог:

Для расчета средней арифметической величины в интервальном вариационном ряду необходимо: 1) Закрыть имеющиеся открытые интервалы группировки. 2) Найти середины каждого интервала, т. е. привести интервальный ряд к дискретному виду. 3) Найти произведение середин интервалов на соответствующие частоты (частости).

- Средний возраст депутатов данной фракции.

Дата добавления: 2015-07-11