|
Читайте также: |
К относительным показателям вариации относятся:
1. Коэффициент квартильной вариации, который вычисляется по формуле:
2. Коэффициент осцилляции: 
.
3. Коэффициент вариации: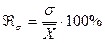 
исходная совокупность считается однородной по изучаемому признаку, если коэффициент вариации меньше 33%. В этом случае средняя величина объективно представляет свою исходную совокупность. Пример вычисления показателей вариации:
| Возраст депутата (полных лет) (X) | Численность депутатов (кол-во человек) (ƒ) | Середины интервалов (X) | 
| 
| 
|
| 20-29 | 24,5 | 23,2 | 23,2 | 538,24 | |
| 30-39 | 34,5 | 13,2 | 211,2 | 2787,84 | |
| 40-49 | 44,5 | 3,2 | 89,6 | 286,72 | |
| 50-59 | 54,5 | 6,8 | 1387,2 | ||
| 60-69 | 64,5 | 16,8 | 117,6 | 1975,68 | |
| Итог: | 645,6 | 6975,68 |
; R=69-20=49 (лет); 
=7,9(лет);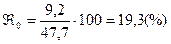 
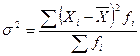=6975,68/82=85,07; 
;
В среднем возраст каждого депутата отличается от среднего возраста для депутатов данной фракции на 9,2 лет. Данная совокупность депутатов считается однородной по возрасту, т. к. коэффициент вариации меньше 33%.
Дата добавления: 2015-07-11; просмотров: 61 | Нарушение авторских прав