Общая схема исследования функции

Считаем, что исследовать функцию – это означает:

1. Найти область существования (определения) функции;

2. Отметить (если они есть) особенности функции (периодичность, четность и нечетность, сохранение знака), найти точки пересечения графика функции с осями координат;

3. Исследование поведения функции в граничных и несобственных точках.

4. Указать вертикальные и горизонтальные асимптоты и найти наклонные асимптоты или убедиться в их отсутствии;

5. Найти участки возрастания и убывания функции, определить локальные и краевые экстремумы;

6. Определить наибольшее и наименьшее значения функции;

7. Найти интервалы, на которых функция выпукла вверх или вниз, определить точки перегиба.

8. По результатам пунктов 1-7 исследований функции строится ее график.

Приведем краткие комментарии к каждому пункту схемы исследования функции 1-8.

1. Для нахождения области существования заданной функции, необходимо исходить из области определения основных элементарных функций (смотри §1).

2. Для определение периода, четности или нечетности функции смотри §1. Точки пересечения с осью 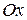определяются из соотношения 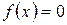. Точки пересечения с осью 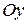определяются из условия .

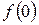3. Если граничные точки области определения функции принадлежат ей, то нужно найти значения функции в этих точках. В некоторых случаях, область определения выглядит как объединение областей, т.е. граничными точками область определения функции разделяется на подобласти, поэтому также нужно найти значение функции во всех граничных точках подобластей, принадлежащих области определения (закрытые множества – отрезки). Если граничные точки не принадлежат области определения (открытые множества – интервалы), то нужно найти односторонние пределы (слева или справа от граничных точек) значений функций в этих точках, включая и несобственные точк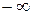и и .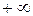

4. Для определения вертикальной, горизонтальной или наклонной асимптот смотри п.4.1, §4.;

5. Для определения интервалов возрастания и убывания функции воспользуйтесь утверждением 1 п.4.2, §4., чтобы определить локальные и краевые экстремумы воспользуйтесь замечанием 1 или утверждением 4 п.4.3, §4. Также нужно обратить внимание на замечание 2 п.4.3, §4 в случае, если в некоторой точки области определения производная не имеет смысла.

6. Для определения наибольшего и наименьшего значений функции воспользуйтесь п.4.4, §4;

7. Для определения интервалов, на которых функция выпукла вверх или вниз воспользуйтесь утверждением 5, п.4.5, §4. Вообще, чтобы точка была точкой перегиба, необходимо чтобы функция была дважды дифференцируема в окрестности этой точки (не обязательно в самой) и выполнение утверждений 6,7,8 п.4.5, §4, тогда только она является точкой перегиба, а в остальных случаях она не будет точкой перегиба. Поэтому для определения точек перегиба воспользуйтесь замечанием 3 п.4.5, §4.

8. Прежде чем строить график, сначала на декартовой системе координат укажите все точки (экстремума, перегиба, пересечения с осями со значениями, наибольшие и наименьшие значения). Затем нарисуйте асимптоты, если они есть. После, эскизы возрастаний и убываний с перегибами, где необходимо, а потом и сам график.

Дата добавления: 2015-07-11