
Читайте также:
|
Пример 1. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Согласно нашей схеме исследования приступим к решению.
1) Данная функция является элементарной, т.к. она получается из элементарных степенных функций как их отношение. Известно, что знаменатель дроби не должен обращаться в нуль, т.е.  . А это в свою очередь означает, что
. А это в свою очередь означает, что  . Поэтому областью определения будет
. Поэтому областью определения будет  кроме точки
кроме точки 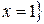 или можно записать
или можно записать  .
.
2) Функция не является ни четной, ни нечетной. Покажем это,
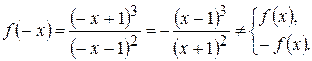
Функция  не является периодической. Покажем это,
не является периодической. Покажем это,
 ,
,
отсюда видно, что  , это в свою очередь показывает, что наша функция не является периодической.
, это в свою очередь показывает, что наша функция не является периодической.
Данная функция не сохраняет знака, т.к. при различных точках из области ее определения она может принимать как положительные, так и отрицательные значения.
Определим точки пересечения функции с осями координат:
с осью 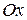 :
:  . Следовательно, точкой пересечения будет точка с координатами
. Следовательно, точкой пересечения будет точка с координатами  ;
;
с осью 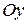 :
:  при
при  . Следовательно, точкой пересечения будет точка с координатами
. Следовательно, точкой пересечения будет точка с координатами 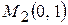 .
.
3) Точка  не принадлежит области определения. Рассмотрим поведение функции в окрестности этой точки, т.е. найдем пределы при
не принадлежит области определения. Рассмотрим поведение функции в окрестности этой точки, т.е. найдем пределы при 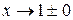 :
:
 ,
,

а также найдем пределы при  :
:


4) Проверим, является ли прямая  асимптотой графика функции
асимптотой графика функции  при
при 
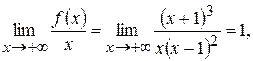


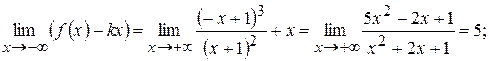
т.к. односторонние пределы попарно совпадают, поэтому прямая  является асимптотой графика функции (причем наклонной).
является асимптотой графика функции (причем наклонной).
Аналогично проверяем, является ли при  прямая
прямая 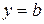 горизонтальной асимптотой графика функции
горизонтальной асимптотой графика функции  при
при  , т.е.
, т.е.


в данном случае, как мы видим, пределы являются бесконечными, различными и  , поэтому график функции не имеет горизонтальной асимптоты.
, поэтому график функции не имеет горизонтальной асимптоты.
Вертикальной асимптотой графика функции будет прямая  , т.к.
, т.к.
 и
и  .
.
5) Определим теперь интервалы возрастания и убывания функции, воспользовавшись утверждением 1, п.4.2. Для этого необходимо найти производную функции  . Согласно правилу нахождения производной
. Согласно правилу нахождения производной  , имеем
, имеем  . Как мы видим решением уравнения
. Как мы видим решением уравнения  являются точки
являются точки  . Производная в точке
. Производная в точке  не существует, но также точка
не существует, но также точка  не принадлежит области определения, поэтому дополнительных исследований не обязательно (она не является ни точкой излома, ни точкой возврата).
не принадлежит области определения, поэтому дополнительных исследований не обязательно (она не является ни точкой излома, ни точкой возврата).
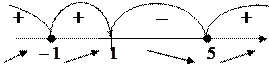 Рисунок 2.
Рисунок 2.
| Далее, разделяем нашу числовую прямую этими точками и точкой  , затем исследуем поведение функции , затем исследуем поведение функции  (смотри рис.2), причем знак определяем у функции (смотри рис.2), причем знак определяем у функции 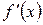 . Таким образом, из рисунка видно, что функция убывает только в интервале . Таким образом, из рисунка видно, что функция убывает только в интервале 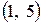 , а в интервалах , а в интервалах  возрастает. возрастает.
|
Следует отметить, что точки  ,
,  являются критическими точками функции. Из рисунка 1 видно, что производная меняет знак в точках
являются критическими точками функции. Из рисунка 1 видно, что производная меняет знак в точках  . Т.к.
. Т.к.  не принадлежит области определения, то она не является ни минимумом, ни максимумом функции, а в точке
не принадлежит области определения, то она не является ни минимумом, ни максимумом функции, а в точке  наблюдается локальный минимум. Значение функции
наблюдается локальный минимум. Значение функции  . Поэтому, точка с координатами
. Поэтому, точка с координатами  является точкой минимума, или записывают
является точкой минимума, или записывают  .
.
6) Функция  непрерывна на всем
непрерывна на всем  , кроме точки
, кроме точки  , поэтому говорить о наибольшем и наименьшем значении функции не имеет смысла, т.к. функция рассматривается не на конечном интервале.
, поэтому говорить о наибольшем и наименьшем значении функции не имеет смысла, т.к. функция рассматривается не на конечном интервале.
7) Интервалы выпуклости будем искать, воспользовавшись утверждением 5.
|
Рисунок 3.
 ,
решением которого будет точка
,
решением которого будет точка  . Как следует из утверждения 5,
. Как следует из утверждения 5,
функция в интервале  выпукла вверх, а в интервалах
выпукла вверх, а в интервалах  выпукла вниз (смотри рис.3). Поэтому точкой перегиба является точка
выпукла вниз (смотри рис.3). Поэтому точкой перегиба является точка  , что подтверждается также утверждением 8, т.к.
, что подтверждается также утверждением 8, т.к.  , а
, а  .
.
Отметим еще очень важные замечания.
1.Хотя, согласно утверждению 2, точка  должная быть точкой экстремума, т.к.
должная быть точкой экстремума, т.к. 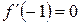 , но это не так. Точка
, но это не так. Точка  является критической точкой, но локального экстремума в ней нет. Здесь важно понимать, что
является критической точкой, но локального экстремума в ней нет. Здесь важно понимать, что  не говорит о том, что
не говорит о том, что  точка экстремума, а вот если известно, что
точка экстремума, а вот если известно, что  точка экстремума, то обязательно выполняется
точка экстремума, то обязательно выполняется  .
.
2. Если посмотреть на график (смотри рис.3), то можно подумать, что точка  является точкой перегиба, но это не так, согласно определению, это точка локального минимума.
является точкой перегиба, но это не так, согласно определению, это точка локального минимума.
Данные этапы решения удобно представлять в виде таблицы 1.
Таблица 1
| Функция График изображен на рисунке 4. | 
| |
| Область определения |  . .
| |
| Особенности | нет | |
| Точки пересечения с осями координат |  , , 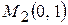 . .
| |
| Значения на границе, в точках разрыва и несобственных |  , ,
 
| |
| Асимптоты | наклонная:  , вертикальная: , вертикальная:  . .
| |
| Интервалы | убывания: 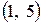 , возрастания: , возрастания:  . .
| |
| Экстремумы |  . .
| |
| Наибольшие и наименьшие значения | нет | |
| Интервалы выпуклости | вниз:  , вверх: , вверх:  . .
| |
| Точки перегиба |  . .
|
 Рисунок 4.
Рисунок 4.
| Рисунок 5. |
При рассмотрении следующего примера, мы уже не будем так расписывать решение, а заполним только таблицу.
Пример 2. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Имеем
Дата добавления: 2015-07-11; просмотров: 105 | Нарушение авторских прав