Условия выпуклости. Точки перегиба.

Функция называется выпуклой вниз (или вогнутой вверх) на интервале , если для любых точек и 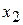этого интервала и любых чисел и 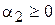таких, что , верно неравенство

(4.5.1)

Рисунок 1

Геометрический смысл выпуклости вниз функции на интервале заключается в том, что точки любой дуги графика функции расположены не выше хорды, стягивающей эту дугу (рис.1). Если функция выпукла вниз на некотором интервале, то ее график тоже называют выпуклым вниз.

Если при тех же условиях относительно выполняется неравенство

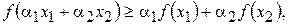(4.5.2)

то функция называется выпуклой вверх (или вогнутой вниз).

В том случае, когда при и неравенство (4.5.1) или (4.5.2) является строгим, функция называется строго выпуклой вниз или соответственно строго выпуклой вверх на интервале.

Всякий интервал, на котором функция (строго) выпукла (вниз или вверх), называется интервалом (строгой) выпуклости (вниз или вверх соответственно).

Утверждение 5 (условия выпуклости). Пусть функция дважды дифференцируема на . Тогда

		выпукла вниз,
		выпукла вверх,
		строго выпукла вниз,
		строго выпукла вверх.

Пусть функция определена в некоторой окрестности точки , за исключением, быть может, самой точки . Если существуют интервалы

и

на одном из которых строго выпукла вниз, а на другом строго выпукла вверх, то говорят, что при переходе через точку функция меняет направление выпуклости.

Пусть функция определена в некоторой окрестности точки , непрерывна в точке и имеет в этой точке конечную или бесконечную производную. Тогда, если функция при переходе через точку меняет направление выпуклости, то точка называется точкой перегиба функции . В этом случае точку с координатами называют точкой перегиба графика функции .

Точки перегиба функции следует искать среди критических точек ее первой производной.

Утверждение 6 (необходимые условия существования точки перегиба). Если точка является точкой перегиба функции , то либо , либо не существует.

Утверждение 7 (достаточные условия существования точки перегиба с использование второй производной). Пусть функция дифференцируема в точке и дважды дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки . Тогда точка является точкой перегиба, если существует окрестность точки , в которой либо

при и при

либо

при и при

В этом случае принято говорить, что при переходе через точку вторая производная меняет знак.

Утверждение 8 (условия существования точки перегиба с использование производных высших порядков). Пусть функция имеет в точке производные до порядка включительно, и пусть

а

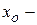тогда если нечетное число, то точка перегиба; если же четное число, то не является точкой перегиба.

Замечание 3. В частности, если

а

то 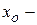точка перегиба функции .

Дата добавления: 2015-07-11