Экстремумы функции

Точка называется точкой локального максимума функции , если существует окрестность точки , для всех точек которой верно неравенство .

Если для всех 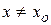из некоторой окрестности точки верно строгое неравенство , то точка называется точкой строгого локального максимума функции .

Аналогично, если в некоторой окрестности точки выполняется неравенство , то точка называется точкой локального минимума; если для всех 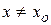из некоторой окрестности точки верно строгое неравенство , то точка называется точкой строгого локального минимума.

Для краткости слово «локальный» часто опускают и пишут просто «точка минимума» или «точка максимума».

Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках – ее экстремумами.

Точки, в которых функция определена, а производная функции равна нулю или не существует, называют критическими точками функции. Экстремумы функции следует искать среди ее критических точек.

Утверждение 2. (необходимые условия экстремума) Если точка является точкой экстремума функции , то либо , либо 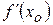не существует.

Утверждение 3. (достаточные условия строгого экстремума с использованием первой производной). Пусть дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки , в которой, однако, функция непрерывна. Тогда точка является точкой строгого максимума, если существует окрестность точки , в которой

при и при .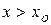

Если же

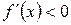при и при ,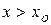

то точка является точкой строгого минимума.

Замечание 1. На самом деле при нахождении (определении) экстремумов исследуется знак производной, т.е., если при переходе через точку (принадлежащая области определения) производная меняет знак, то экстремум есть (причем, если с «+» на «–», то 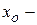точка строгого максимума; если с «–» на «+», то 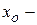точка строгого минимума), а если ее знак при этом не меняется, то экстремума нет. Если же точка не принадлежит области определения, хотя производная меняет знак, она не является ни точкой минимума, ни точкой максимума.

Утверждение 4. (условия строгого экстремума с использованием производных высших порядков). Пусть функция имеет в точке производные до порядка 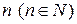включительно. Тогда, если

а

то при четном точка является точкой строгого экстремума, причем точкой максимума, если 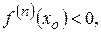и точкой минимума, если при нечетном экстремума в точке нет.

В частности, если

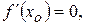а

то в точке имеется строгий максимум в случае и строгий минимум в случае .

Замечание 2. В некоторых случаях не для всех точек из области определения существуют производные (смотри §3, п.3.3). Поэтому, чтобы определить для таких точек локальное поведение графика функции (т.е. являются ли эти точки точками излома или возврата), необходимо дополнительное исследование с помощью поведения касательных к графику функции в указанных точках (смотри §3, п.3.3).

Дата добавления: 2015-07-11