Наибольшее и наименьшее значения функции

Для функции, непрерывной на отрезке, существуют на этом отрезке точка, в которой функция принимает наибольшее значение, и точка, в которой функция принимает наименьшее значение (теорема Вейерштрасса).

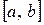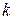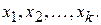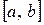Пусть функция непрерывна на отрезке и имеет на нем локальных максимумов в точках Тогда наибольшее значение функции на отрезке наибольшему из чисел

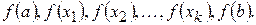
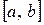Аналогично, если функция непрерывна на отрезке и имеет на нем локальных минимумов в точках 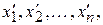то ее наименьшее значение на этом отрезке равно наименьшему из чисел

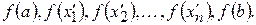
Дата добавления: 2015-07-11